凸包

二维凸包¶

定义¶

凸多边形：所有内角大小都在 \([0, \pi]\) 范围内的简单多边形

凸包：在平面上能够包含所有给定点的最小凸多边形

对于凸包，想象在给定平面上用一个橡皮筋去套住所有给定点后围成的图形即可。凸包是能围住所有点的所有多边形中周长最小的多边形，从下图¹中可以看出来：

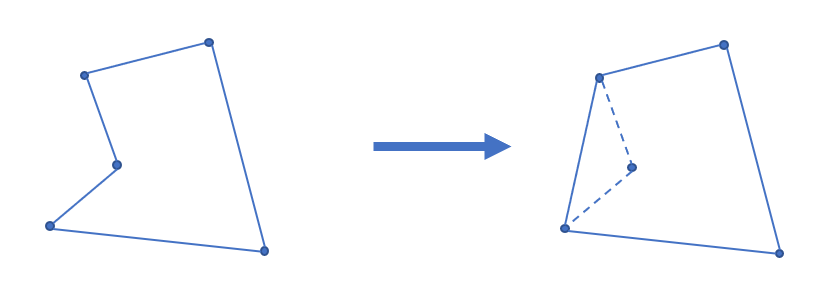
算法¶

暴力穷举法¶

最左下角的点一定在凸包上，于是我们将这个点加入凸包上的点集，枚举点集中的点，求出其他每个点与当前点组成的直线的斜率，将斜率最大和最小的两个点加入点集即可求出凸包上的点，复杂度 \(\mathcal{O}(nm)\) ，\(m\) 为凸包上的点的数量。

Jarvis 步进法¶

同样从左下角的点开始，按照逆时针方向逐个找凸包上的点，一步一个点，因此叫步进法。

假设当前已经找到了前 3 个点，分别是 \(p_0, p_1, p_2\) ，那么 \(p_2\) 到下一个点构成的向量与向量 \(\overrightarrow{p_1 p_2}\) 的夹角一定最小，如下图²所示

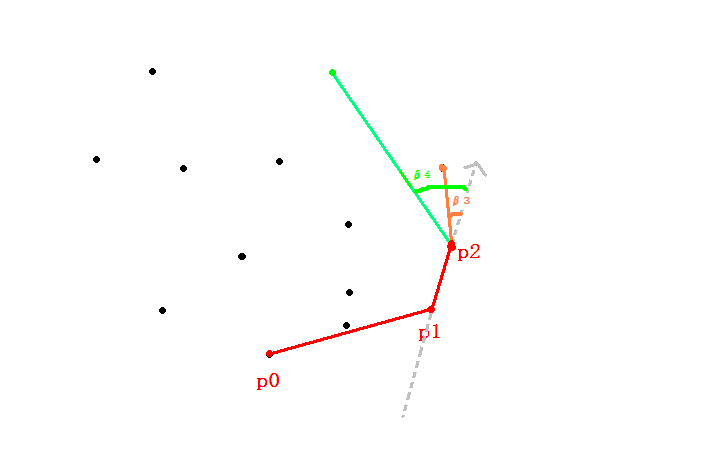
于是之后我们只需要利用 \(\cos\beta = \dfrac{\vec{u} \cdot \vec{v}}{|\vec{u} \times \vec{v}|}\) 求出下一个点即可，复杂度 \(\mathcal{O}(nm)\) ，\(m\) 为凸包上的点的数量。

Andrew 算法¶

从左下角的点开始，按照从左往右、从下到上的顺序先寻找下凸包上的点，然后再从右上角的点出发，按照从右往左、从上到下的顺序寻找上凸包上的点，因此，首先将所有点按照以横坐标为第一关键字、纵坐标为第二关键字进行排序。

我们以下图³为例：

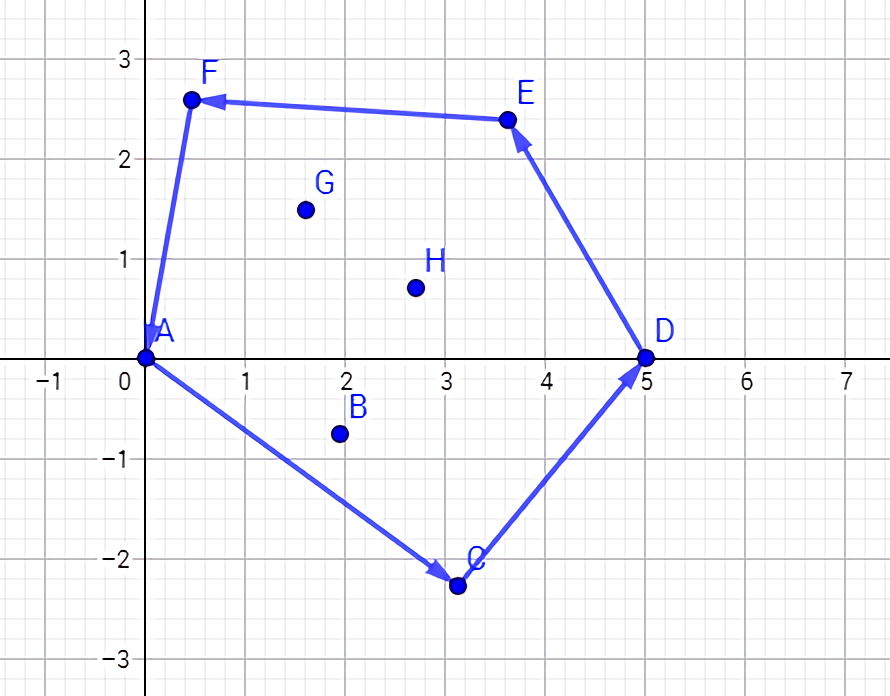
观察可以发现，凸包上相邻三个点（分别设为 \(P_1, P_2, P_3\) ）组成的内夹角一定小于 \(\pi\) ，换而言之，如果是下凸包的话 \(P_2\) 必然在线段 \(P_1 P_3\) 的下方，因此我们可以按照上面所说的顺序，先将前两个点加入点集（栈），然后判断用当前枚举到的第三个点判断是否满足上述条件，如不满足就将栈顶的点弹出，一直到满足上述条件为止，枚举完所有的点也就找到了下（上）凸包上的点了。

至于如果判断是否满足条件，就需要用到点积，以上图中的点 \(A,B,C\) 为例，\(B\) 点在 \(AC\) 上方就会有 \(\overrightarrow{AB}\cdot\overrightarrow{BC}<0\)，如果是等于 0 的情况就说明 \(B\) 在 \(AC\) 上，这种情况下一般也会将 \(B\) 点去掉，因而判断条件为 \(\overrightarrow{AB}\cdot\overrightarrow{BC}\le 0\)

需要注意的是，由于排序和凸包内部的点所处线段上下方向不同的问题，求解上凸包时需要将所有点倒着枚举一遍，这样就不需要更改判断条件了。

复杂度 \(\mathcal{O}(n\log n)\)，瓶颈在于排序。

struct Point {
    double x, y;

    Point operator-(Point &t) const { // - 重载为求解向量
        return (Point){ x - t.x, y - t.y };
    }
} cov[N];

void Andrew() {
    std::sort(points.begin(), points.end(), [](Point& a, Point& b) -> bool {
        return (a.x == b.x) ? (a.y < b.y) : (a.x < b.x);
    }); // 排序

    auto cross = [](Point a, Point b) -> double { // 计算点积
        return a.x * b.y - a.y * b.x;
    };

    int tot = 0, tmp;
    for (int i = 0; i < n; ++i) { // 先求解下凸包
        while (tot >= 2 &&
            cross(cov[tot - 2] - cov[tot - 1], cov[tot - 1] - points[i]) <= 0) {
            tot--;
        }
        cov[tot++] = points[i];
    }

    tmp = tot;
    for (int i = n - 2; i >= 0; --i) { // 再求解上凸包
        while (tot - tmp >= 1 &&
            cross(cov[tot - 2] - cov[tot - 1], cov[tot - 1] - points[i]) <= 0) { // 下凸包上的点再计算一遍不会影响结果
            tot--;
        }
        cov[tot++] = points[i];
    }
}

Graham 扫描法¶

Graham 扫描法与 Andrew 算法的不同在于它是从纵坐标最小的点开始，将它作为原点，以其它点到原点的极角大小为关键字进行排序的，相比之下，Andrew 算法会更 intuitive 一些。

复杂度的瓶颈同样在于排序，为 \(\mathcal{O}(n\log n)\)

struct Point {
    double x, y, ang;

    Point operator-(Point &t) const { // - 重载为求解向量
        return (Point){ x - t.x, y - t.y };
    }
} cov[N];

void Graham() {
    for (int i = 1; i < n; ++i) { // 求出纵坐标最小的点
        if (points[i].y < points[0].y ||
           (points[i].y == points[0].y && points[i].x < points[0].x)) {
            std::swap(points[0], points[i]);
        }
    }
    for (int i = 1; i < n; ++i) { // 求出每个点的极角
        points[i].ang = std::atan2(points[i].y - points[0].y, points[i].x - points[0].x);
    }

    std::sort(points.begin(), points.end(), [](Point& a, Point& b) -> bool {
        return a.ang < b.ang;
    }); // 排序

    auto cross = [](Point a, Point b) -> double { // 计算点积
        return a.x * b.y - a.y * b.x;
    };

    int tot = 0, tmp;
    for (int i = 0; i < n; ++i) { // 先求解下凸包
        while (tot >= 2 &&
            cross(cov[tot - 2] - cov[tot - 1], cov[tot - 1] - points[i]) <= 0) {
            tot--;
        }
        cov[tot++] = points[i];
    }

    tmp = tot;
    for (int i = n - 2; i >= 0; --i) { // 再求解上凸包
        while (tot - tmp >= 1 &&
            cross(cov[tot - 2] - cov[tot - 1], cov[tot - 1] - points[i]) <= 0) { // 下凸包上的点再计算一遍不会影响结果
            tot--;
        }
        cov[tot++] = points[i];
    }
}

三维凸包¶

TODO

凸包