公平组合游戏
公平组合游戏(Impartial Combinatorial Games, ICG)指的是:
- 两人共同参与,轮流行动,均知道游戏的完整信息
- 在某一状态下可以做出的决策集合仅与当前的局面有关,与游戏者无关
- 经过有限步数后一定会以非平局结束游戏,一般是以某一玩家无法继续行动为结束点
公平组合游戏有多种,其中最经典的是 Nim 游戏,并且其他的公平组合游戏都可以转化为 Nim 游戏。
Nim 游戏¶
\(n\) 堆物品,每堆有 \(a_i\) 个,两个玩家轮流取走任意一堆的任意个物品,但不能不取。
取走最后一个物品的人获胜,也就是玩家无法行动的时候即为输。
不妨假设两位玩家都是绝顶聪明,行动必采取最优策略。在这种情况下,如果每种局面都存在最优策略,那么当初始局面给定时一定可以确定先手/后手必输,因此我们先考虑是否一定存在最优策略。
可以发现,所有局面对应的结束局面都是:
- \(a_i = 0, \forall i = 1, 2, \dots. n\) 此时先手必输
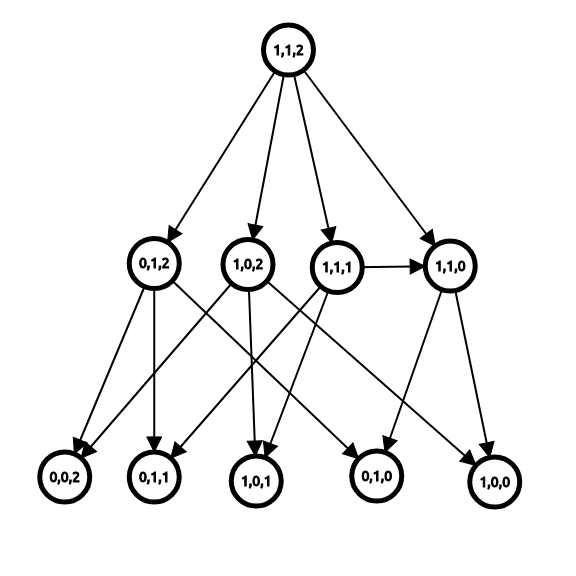
我们在此基础上加石子,枚举该局面可能的父局面,显然这些父局面都是先手必赢的。依此类推,不断地加石子必然可以得到初始局面,不难发现这个过程得到的是一张单起点单终点的有向无环图,其中每个结点对应某个局面(称为状态),每条边对应一种行动,我们将这个图称为博弈状态图。
先给出两个定义:
- P-position: 当前局面先手必输,后手必赢
- N-position: 当前局面先手必赢,后手必输
显然 \((0, 0, 0)\) 是 P-position,于是我们可以标记它的父节点为 N-position,自底向上标记,如果某个结点存在一个子节点为 P-position,那么它一定是 N-position,否则为 P-position(不存在最优策略)。这样一来,整张图的所有结点必然都会有一个标记,因此对于任意局面,如果每次采取最优策略那么它的结局从一开始就是确定好了的。
之后我们考虑如何确定某一局面是 P-position 还是 N-position。
最简单粗暴的办法当然是在这张图上自下而上遍历,由于会有重复的状态所以还需要记忆化,这样时间复杂度和空间复杂度都是 \(O(\prod^{i=1}_{n}a_i)\) 的。
这时候你也许会认为没有更优的办法了,但是,回想一下之前标记的过程:
如果某个结点存在一个子节点为 P-position,那么它一定是 N-position,否则为 P-position(不存在最优策略)。
直觉告诉我,它一定还存在优化的空间!
事实上,确实有更好的办法,并且理论上应该也是最优的算法,那就是可以利用异或(\(\otimes\))操作 \(O(n)\) 地求解。
结论:如果 \(a_1 \otimes a_2 \otimes \dots \otimes a_n=0\),则先手必败。
使用数学归纳法证明:
- 对于有且仅有的 terminal position \(a_1=a_2=\dots=a_n=0\) ,上述结论显然满足
- 对于任何 N-position \(a_1 \otimes a_2 \otimes \dots \otimes a_n=k \not=0\) ,必然存在某种行动使得它的子局面满足 \(a_1^\prime \otimes a_2^\prime \otimes \dots \otimes a_n^\prime=0\)
- \(k\) 二进制下最高位的 1 必然由某个 \(a_i\) 贡献而来,令 \(a_i^\prime=k \otimes a_i < a_i\) 其余保持不变,此时 \(a_1\otimes \dots \otimes a_i^\prime \otimes \dots \otimes a_n=0\)
- 对于任何 P-position \(a_1 \otimes a_2 \otimes \dots \otimes a_n=0\) ,无论如何行动,它的子局面必然为 \(a_1^\prime \otimes a_2^\prime \otimes \dots \otimes a_n^\prime\not=0\)
- 假设拿 \(a_j\) 中的石子,那么无论拿走多少,\(a_j\) 的二进制位下至少有一位翻转了,最终异或和下的那一位必然变成 1,因此子局面的异或和不可能为 0
自此,我们可以根据异或和判断 P/N-position 。
但是问题来了,异或的操作无论是和 Nim 游戏还是和上面的博弈状态图看上去都风马牛不相及,为什么异或和可以求出某一个局面是 P 还是 N-position 呢?上述的证明使用了数学归纳法,也仅仅是已知结论进行推导它确实成立而已。
一个揭示了有向图游戏和异或操作的本质关联的解释用到了群论2,另外一个更 intuitive 的解释在 John Conway 的 Winning Ways for Your Mathematical Plays 书中有提到(当然我没看过,之后有时间也许会看看这本书?)
SG 函数¶
To be continued......