运算方法与运算器
定点加减法¶
补码加减法¶
- 定点整数:\([x \pm y]_{补} = [x]_{补} \pm [y]_{补} \pmod{2^{n + 1}}\)
- 定点小数:\([x \pm y]_{补} = [x]_{补} \pm [y]_{补} \pmod{2}\)
补码溢出判别¶
- 直接判别法
- 同号相加,结果符号相反
- 异号相加,结果符号与减数相同
- 变形补码判别法
01上溢10下溢
- 进位判别法
- \(V = C_{f} \oplus C_{n-1}\)
- 其中 \(C_f\) 为符号位产生的进位, \(C_{n-1}\) 为最高数值位产生的进位
二进制加法减法器¶
行波进位加减法器:
- \(S_{i} = X_{i} \oplus Y_{i}\oplus C_{i}\)
- \(C_{i + 1} = X_{i}Y_{i} + (X_{i} \oplus Y_{i})C_{i}\)
先行进位加法器 74LS181:
- 进位生成函数 \(G_{i}=X_{i}Y_{i}\),进位传递函数 \(P_{i}=X_{i} \oplus Y_{{i}}\)
- \(S_{i} = P_{i} \oplus C_{i}\),\(C_{i+1} = G_{i} + P_{i}C_{i}\)
- \(C_{n} = G_{n-1} + P_{n-1}G_{n-2} + P_{n-1}P_{n-2}G_{n-3} + \cdots + P_{n-1}P_{n-2}\cdots P_{1}P_{0}C_{0}\)
- 成组进位生成函数 \(G^\star = G_{3} + P_{3}G_{2} + P_{3}P_{2}G_{1} + P_{3}P_{2}P_{1}G_{0}\),成组进位传递函数 \(P^\star = P_{3}P_{2}P_{1}P_{0}\)
- \(C_{4} = G^* + P^* C_{0}\)
74LS182(CLA):
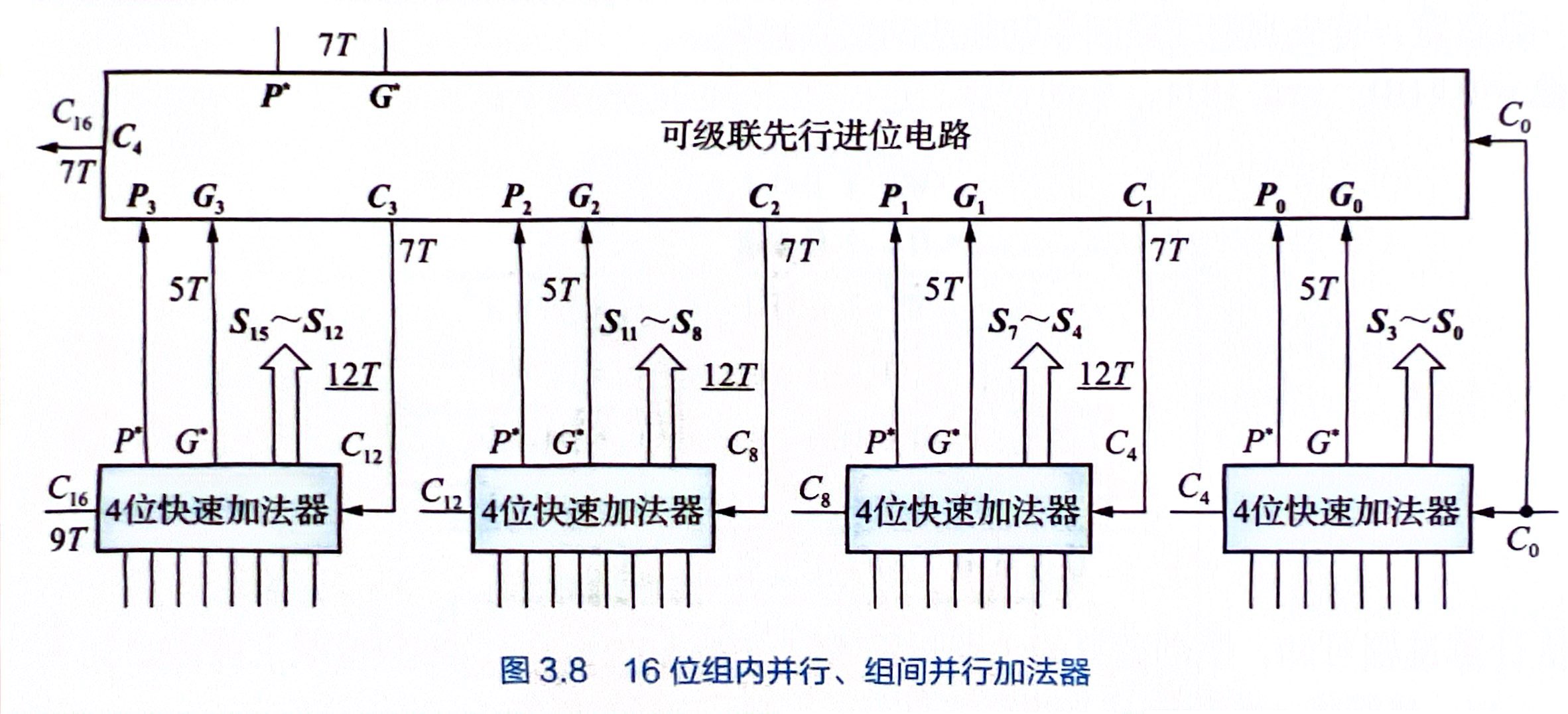
定点乘法¶
原码一位乘法¶

补码一位乘法¶

无符号阵列乘法器¶
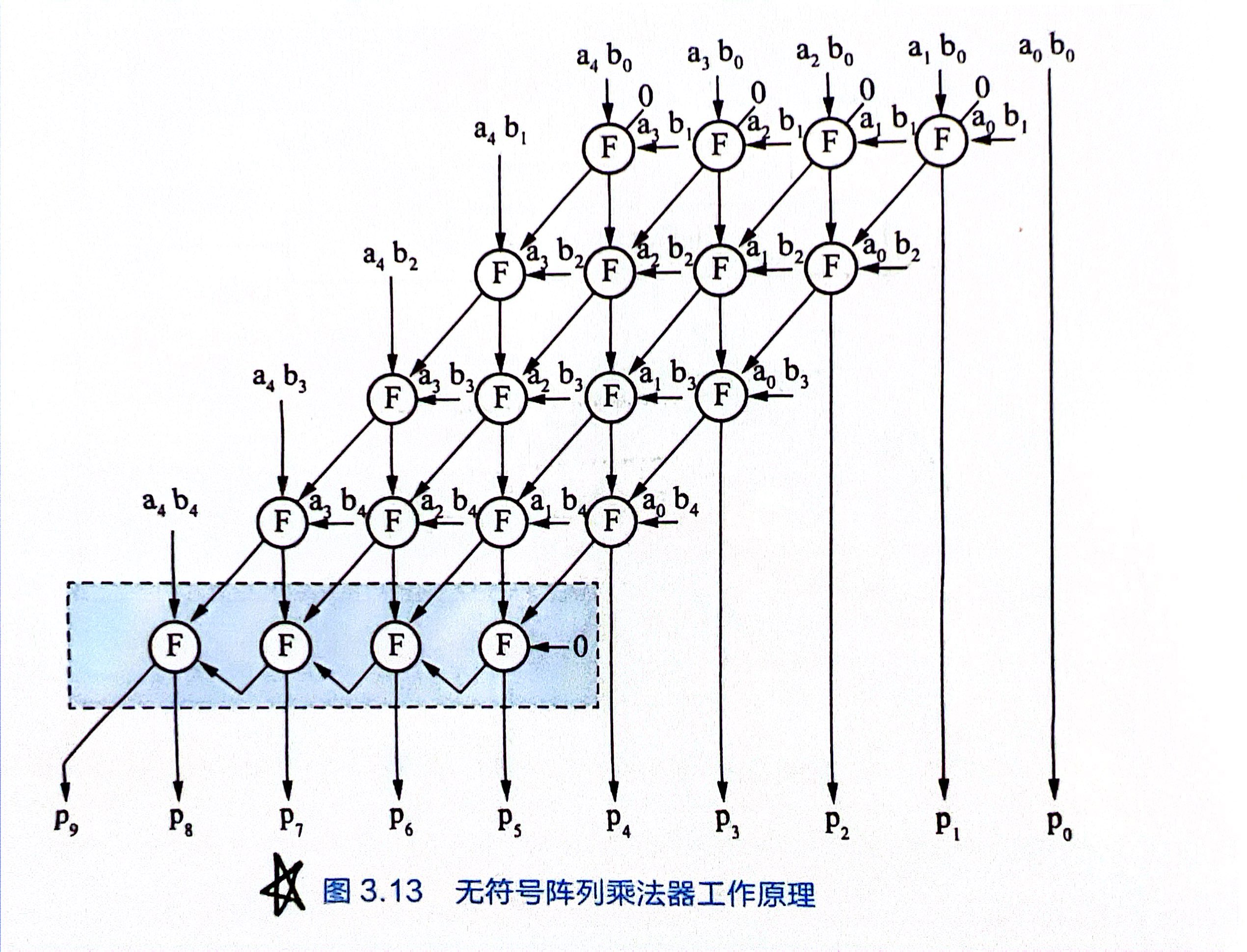
乘法器性能优化:乘法流水线
定点除法¶
原码一位除法¶
原码恢复余数法:
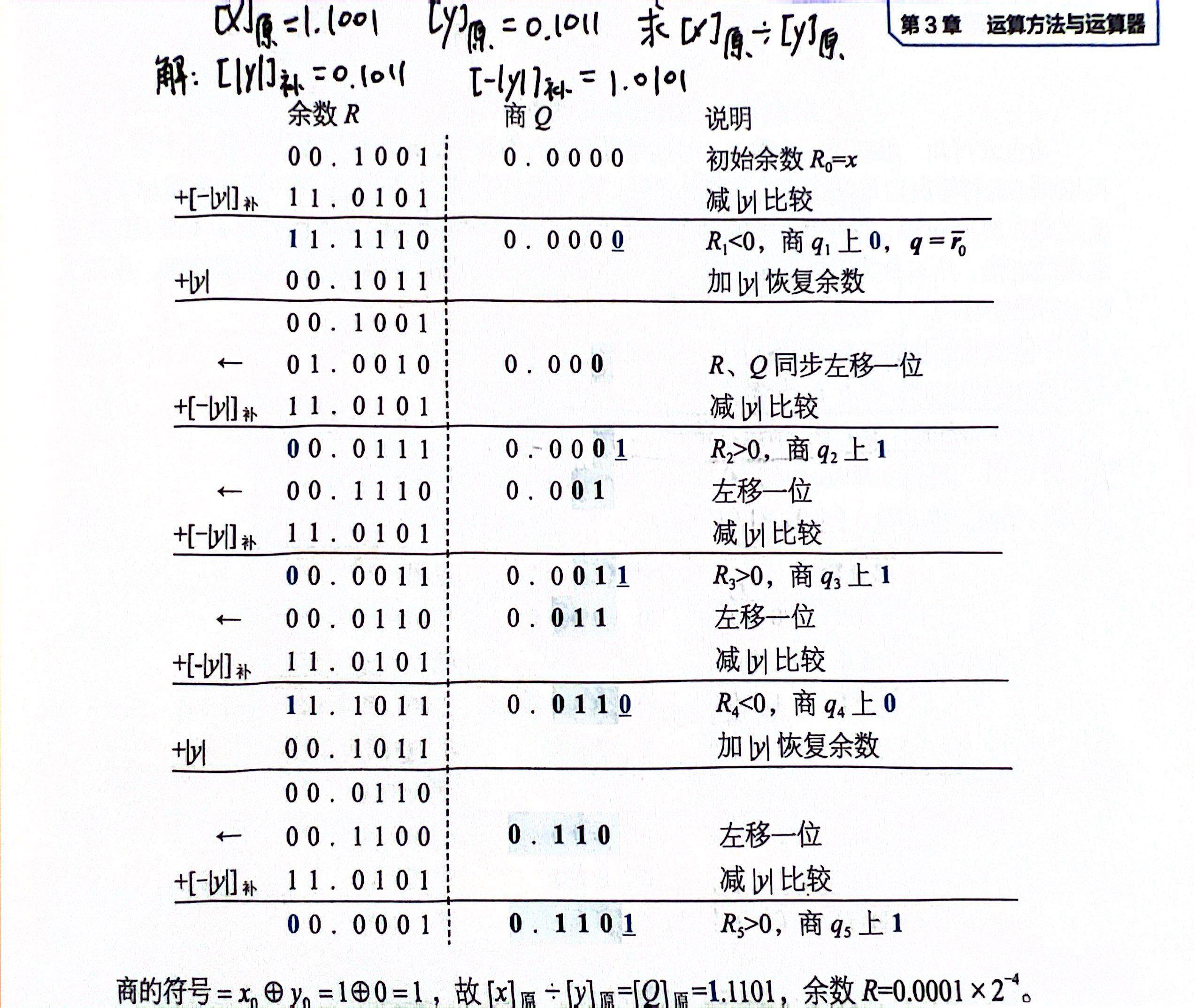
原码不恢复余数法:
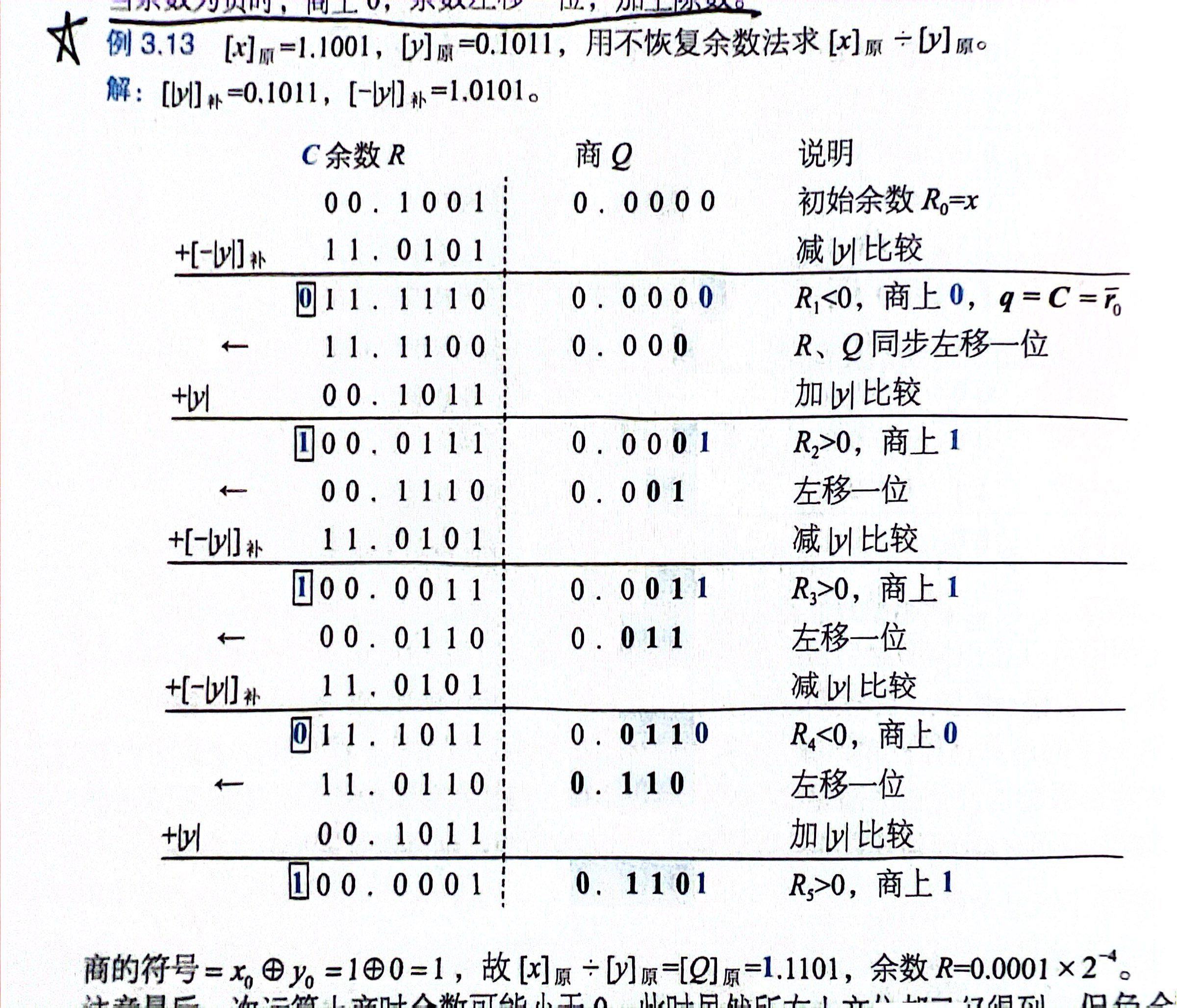
浮点运算¶
浮点数加减法¶
阶码和尾数采用补码表示的浮点加减运算:
- 对阶:小的阶码向大的对齐
- 尾数运算
- 结果规格化
- 舍入
- 末尾恒置 1 法
- 0 舍 1 入法
- 溢出判断:阶码的双符号位
