Skip to content

公钥密码

公钥密码体制的提出

对称密码的问题：

  • 密钥交换（最大）
  • 密钥管理
  • 抵赖

公钥算法的使用方式：

  • 用于加密（公钥加密私钥解密），不需要交换密钥
  • 用于认证（私钥签名公钥验证），可防止抵赖

RSA 算法

RSA原理和实现

RSA 算法的安全性：

  • 取决于分解 \(N\) 的难度
    • 攻击方式：直接分解 \(N\)
    • 建议使用 2048 位
  • 其他攻击方法
    • 间接分解模数 \(n\)
    • 共模攻击
    • 小加密指数攻击
    • 小解密指数的 Wiener 攻击

特点：

  • 教科书式的 RSA 方案是不安全的
  • 速度慢是 RSA 算法的主要缺点
    • 选择特定的 e 值可以大大加快RSA的速度
  • 可用于加密、密钥交换和数字签名

Solovay-Strassen算法

image.png

Miller-Rabin 算法

Miller Rabin

RSA-CRT

利用中国剩余定理加速 RSA

已知密文 \(\mathrm{C}\)、解密密钥 \(d\) 以及 \(p,q\)，利用 CRT 加速解密明文 \(m\) ：

\[ \begin{cases} m \equiv (\mathrm{C} \bmod{p})^{d \bmod{\varphi(p)}} \pmod{p} \\ m \equiv (\mathrm{C} \bmod{q})^{d \bmod{\varphi(q)}} \pmod{q} \end{cases} \]

Rabin 密码

注意这里 \(p,q\) 都是 Blum 素数。

设密文为 \(y\)，公钥 \(n=pq\)，解密即为求解同余式

\[ x^2 \equiv y \pmod{pq} \]

上述同余式等价于

\[ \begin{cases} x^2 \equiv y \pmod{p} \\ x^2 \equiv y \pmod{q} \end{cases} \]

显然 \(y\) 会满足 \(\left( \dfrac{y}{p} \right)=1, \left( \dfrac{y}{q} \right)=1\)，由欧拉判别法则，有

\[ y^{\frac{p-1}{2}} \equiv 1 \pmod{p} \implies y^{\frac{p+1}{2}} \equiv y \pmod{p} \]

因为 \(p=4k+3(k \in \mathbb{N})\)，因此上式等价于 \((y^{\frac{p+1}{4}})^2 \equiv a \pmod{p}\)，于是我们可以得到

\[ \begin{cases} x \equiv \pm y^{\frac{p+1}{4}} \pmod{p} \\ x \equiv \pm y^{\frac{q+1}{4}} \pmod{q} \end{cases} \]

由此，只要知道了 \(n\) 的分解就能直接利用 CRT 解密了，所以 Rabin 密码的安全性仍然基于大整数分解的困难性。

image.png

Diffie-Hellman 算法

Diffie-Hellman 密钥交换和 Elgamal 加密算法

基于离散对数求解困难性。

假设 Alice 和 Bob 互相在不安全信道传递消息，他们首先约定好一个素数 \(p\) 以及本原元 \(g \in \mathbb{Z}_{g}\)，Alice 和 Bob 分别选择一个心仪的整数 \(x\) 和 \(y\)，然后再分别计算好 \(X = g^x \pmod{p}\) 和 \(Y = g^y \pmod{p}\)，之后 Alice 将 \(X\) 发送给 Bob，Bob 将 \(Y\) 发送给 Alice，于是他们约定的密钥即为 \(g^{xy}\)，Alice 只需求出 \(Y^x\) 即可，Bob 则是 \(X^y\)，这样一来便在不安全信道中完成了密钥交换。

需要注意的是，DH 算法无法防止中间人对消息进行截获并篡改，即对 Alice 伪装成 Bob，对 Bob 伪装成 Alice。

Shanks 算法

基础数论#BSGS

有限域上的椭圆曲线

有限域上的椭圆曲线

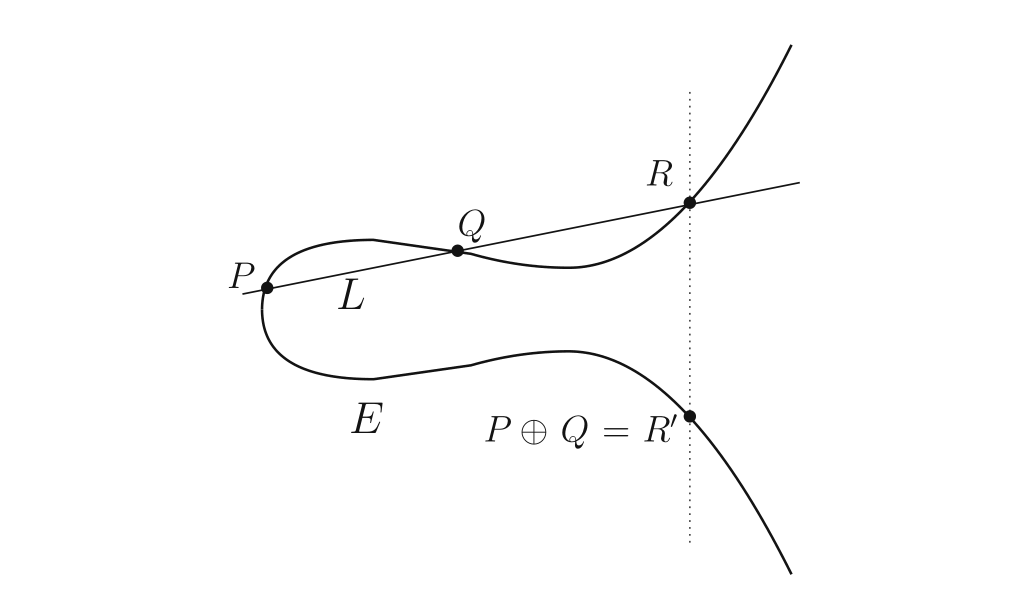
椭圆曲线方程 \(Y^2 = X^3 + AX + B\)，定义其上两点 \(P,Q\) 的和 \(P+Q\) 为直线 PQ 与曲线的第三个交点关于 \(x\) 的对称点，即为下图中的 \(R^\prime\) :

image.png1

已知 \(P,Q\) 的坐标，可以很快求出 PQ 的直线方程，然后将其代入椭圆曲线方程即可求出 \(R\) 的坐标，然后将 \(y_{R}\) 取相反数即可得到 \(R^\prime\)。当 \(P=Q\) 时，不难想到直线 PQ 应该定义为 P 点处的切线。

根据上述定义，当直线 PQ 与 \(y\) 轴平行时或者它是某些特殊的切线时就不存在第三个交点了，为了让上述加法的定义满足封闭性，我们额外定义一个无穷远点 \(\mathcal{O}\)，令上述情况下的 \(P+Q = \mathcal{O}\)，然后考虑一下 \(P+\mathcal{O}\) 的结果，根据上述定义，设 \(P^\prime\) 为 \(P\) 关于 \(x\) 轴的对称点，那么直线 \(P\mathcal{O}\) 与曲线交于点 \(P^\prime\)，然后再将其关于 \(x\) 轴对称，便得到 \(P+\mathcal{O}=P\)，这启发我们 \(\mathcal{O}\) 是上述加法下的单位元。

不难验证，上述椭圆曲线上的点集并上无穷远点，与上述定义的加法构成了一个加法群，并且是阿贝尔群。

但是，仍然存在一类特殊的曲线存在奇点，导致不能构成一个加法群，为了方便起见，我们直接不考虑这一类曲线。于是有限制条件 \(4A^3 + 27B^2 \not=0\)。

由于计算机只能处理离散的数据，因此我们进一步将上述点集以及运算限制在有限域 \(\mathbb{F}_{p}\) 上，于是便成为了有限域上的椭圆曲线问题。

多倍点问题即给出点 \(Q = nP = P+P+P+\cdots\) 和点 \(P\) ，求解对应的 \(n\) 是困难的，类似于求解离散对数问题，于是可以根据这个性质来构造公钥密码。

Elgamal

椭圆曲线 Elgamal 公钥密码体系

SM2

IOS应用安全-加解密算法简述 #国密算法SM2

数字签名

公钥密码的使用和优势：

  • 远程密钥分配
  • 数字签名
    • 思想：私钥加密公钥验证
    • 功能：不可抵赖

先摘要再签名更安全。

PGP

  • 认证：私钥签名保证认证功能防抵赖
    • \(\operatorname{Sig}_{sk_{A}}(\operatorname{H}(M))||M\)
  • 机密性：消息用对称密码加密，对称密钥使用对方的非对称密码下的公钥加密
    • \(\operatorname{EC}_{k_{s}}(M)||\operatorname{EP}_{{pk_{B}}}(k_{s})\)
  • 认证机密性同时满足
    • \(\operatorname{EC}_{k_{s}}(\operatorname{Sig}_{sk_{A}}(\operatorname{H}(M))||M)||\operatorname{EP}_{{pk_{B}}}(k_{s})\)

说明：

  • \(\operatorname{EP}\) 和 \(\operatorname{DP}\) 为非对称加解密
  • \(\operatorname{EC}\) 和 \(\operatorname{DC}\) 为对称加解密
  • \(\operatorname{H}\) 为 Hash 函数
  • \(\operatorname{Sig}\) 和 \(\operatorname{Ver}\) 为签名和认证
  • \(k_{s}\) 为会话密钥（对称）
  • \((pk,sk)\) 为公私密钥对

  1. 图源：An Introduction to Mathematical Cryptography ↩


Comments