分组密码
设计原理¶
分组密码的设计原则:
- 安全性原则
- 现代密码学的设计原理:
- 混乱原则:使加密和密钥的关系尽可能复杂和相关
- 扩散原则:把单个明文位或密钥位的影响尽可能扩大到更多的密文中
- 现代密码学的设计原理:
- 实现原则
现代分组密码算法大多采用迭代密码的方式,乘积密码的思想,轮流使用代换 S 盒和置换 P 盒技术,可以看作伪随机置换:
- S 盒:提供混乱效果
- 规模越大,混乱效果越好,实现效率越低
- P 盒:进行扩散
- 提供雪崩效应,进一步提高混乱效果
评价密码体制的安全性:
- 计算安全性
- 可证明安全性
- 无条件安全
若 \(S_1\) 和 \(S_2\) 是两个密码体制,明密文空间相同,设 \(S_1=(P, P, K_1, E_1, D_1), S_2=(P, P, K_2, E_2, D_2)\),则他们的乘积密码体制 \(S_1\times S_2\coloneq(P, P, K_1\times K_2, E, D)\):
- \(e_{(k_1, k_2)}(x) = e_{k_2}(e_{k_1}(x))\)
- \(d_{(k_1, k_2)}(x) = d_{k_1}(d_{k_2}(x))\)
幂等密码体制:\(S^2=S\)
- 古典密码中的移位、代换、乘法、仿射、置换、维吉尼亚、希尔密码都是幂等的
SPN 网络和 Feistel 结构¶
SPN 网络¶
AES 算法是 SPN 网络的典型代表。
SPN 网络的一轮代换如图:
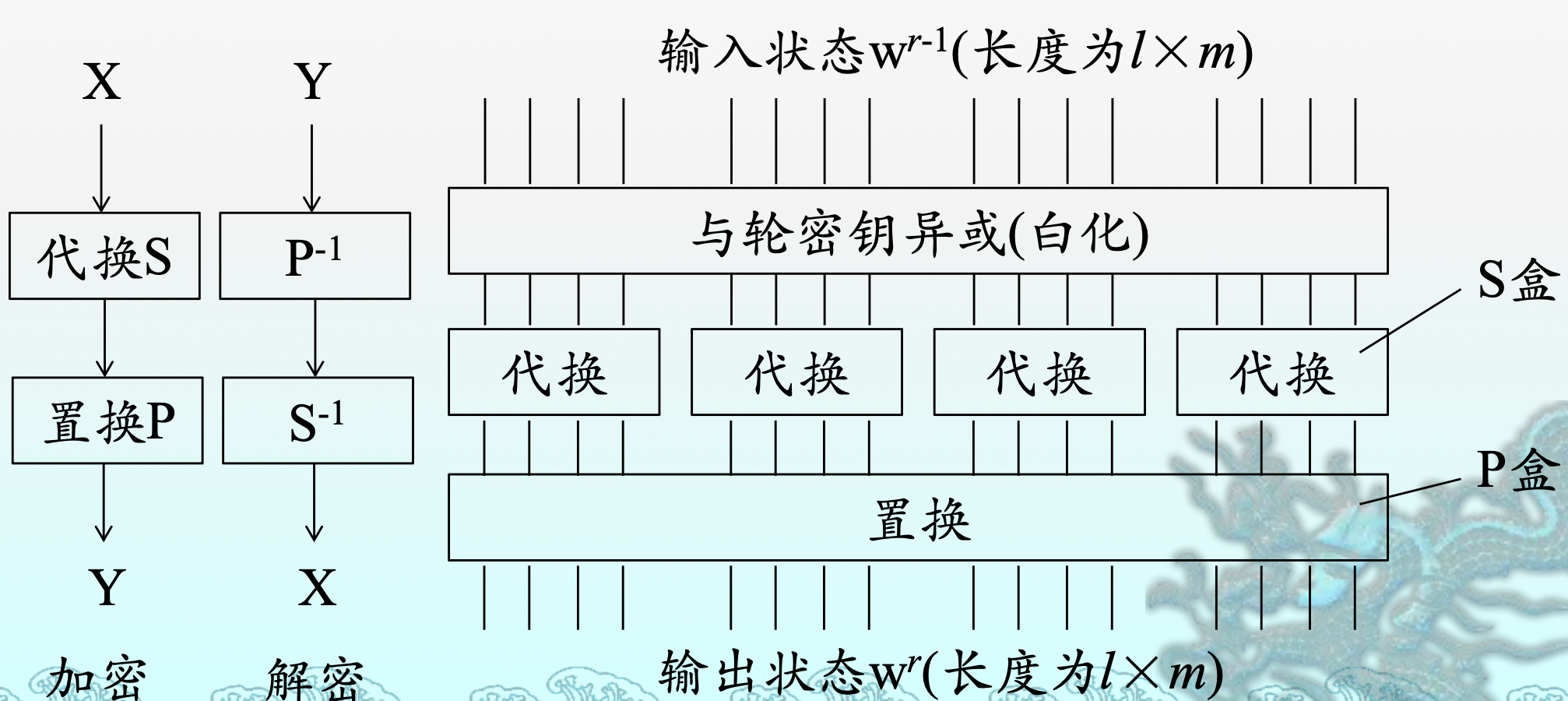
SPN 网络的解密处理:
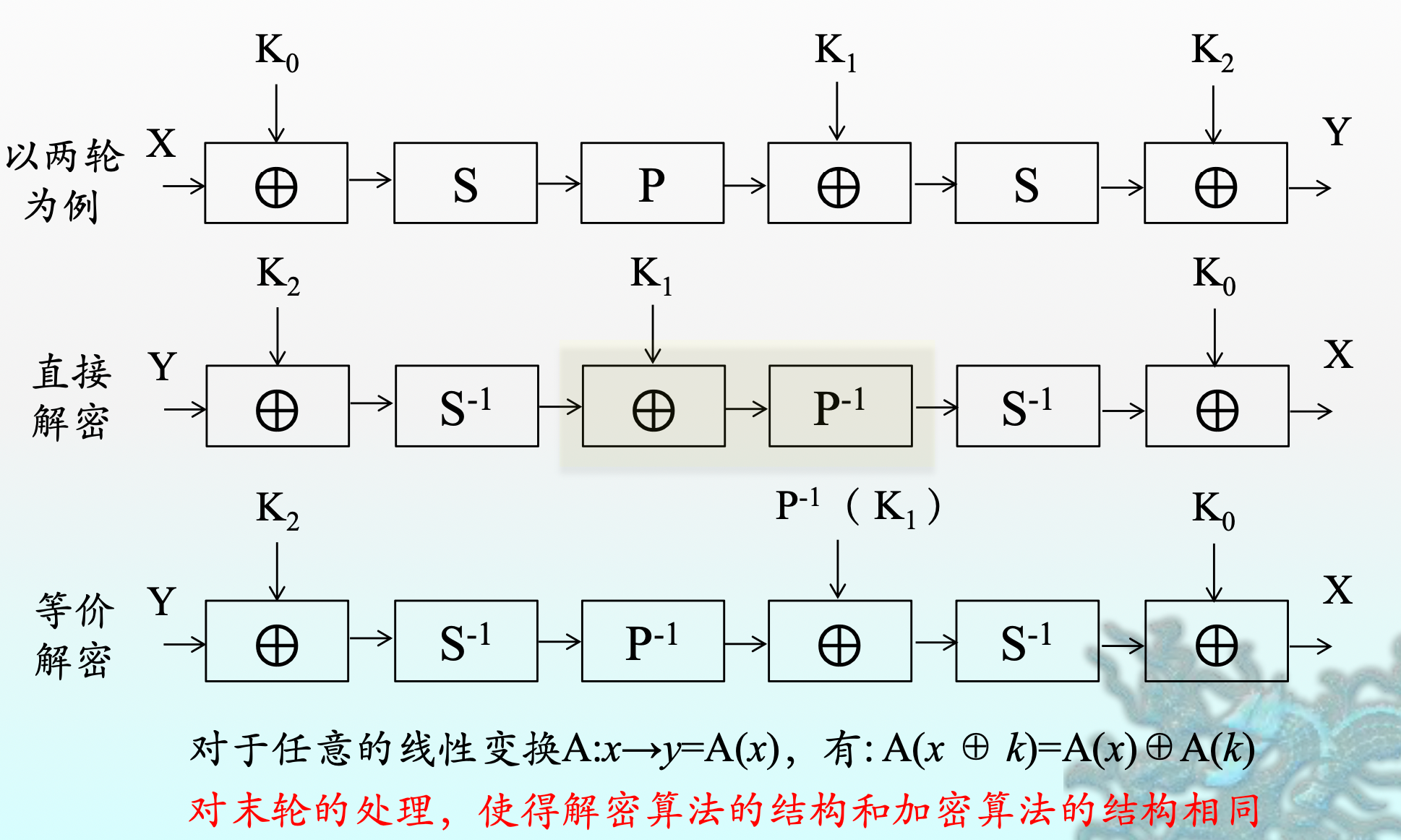
特点:
- 易于软件、硬件实现,高效快速,易于扩展和强化
- 可以通过增大 S 盒的规模来提高安全性,但是会给存储带来困难
- 可以增加轮数来提高混乱程度
- 可以同时使用多个 S 盒和 P 盒进一步提高复杂性
- 加解密结构相似,扩散快,轮函数的过程可逆
Feistel 结构¶
DES、SM4 算法使用的是 Feistel 结构。
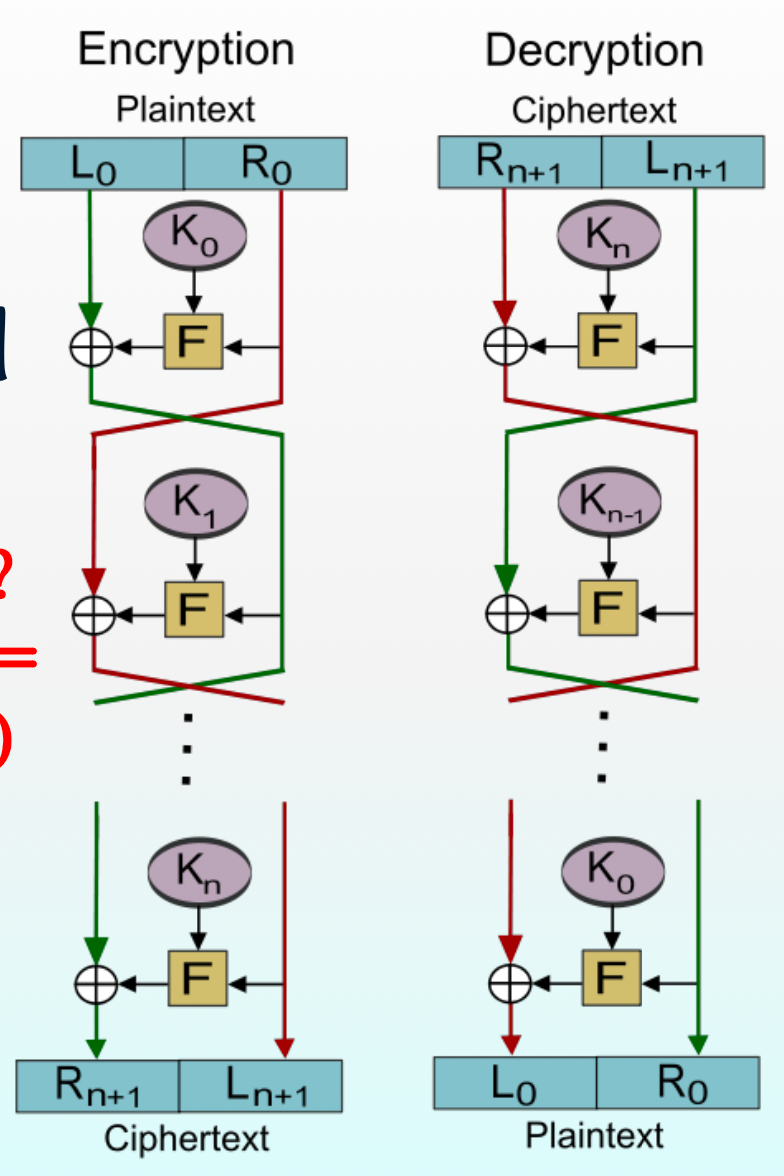
特点:
- 加密、解密过程相同,只是子密钥逆序使用
- 非线形变换 \(f\) 不需要单射
- 扩散较慢
DES 算法¶
DES 算法的安全性有何不足:
- 密钥长度不足
- 存在弱密钥、半弱密钥(密钥有互补性)
由于 DES 是非幂等的密码体制,因此可以通过自身的乘积来提高安全性,但是实现效率低。
AES 算法¶
AES 每次的操作对象是一个 128bit 的明文块,将其表示为一个 \(4\times 4\) 的网格,单个格子的大小为 1 byte.
字节代换 SubBytes¶
即将这个 \(4\times 4\) 的网格中每个格子按照它的值映射成 \(16\times 16\) 大小的 S 盒的元素。
假设当前格子的值为 \((AE)_{\text{16}}\) ,那么它会变成 S_box[(A)_16][(E)_16] 中的元素。
列混合 MixColumns¶
使用 \(\operatorname{GF}(2)[x]/(x^8 + x^4 + x^3 + x + 1)\) 来构造 \(\operatorname{GF}(2^8)\) ,下面用到的运算都在 \(\operatorname{GF}(2^8)\) 上进行。
列混合就是对前面提到的网格的每一列看成一个 \(4\times 1\) 的矩阵,左乘上一个 \(4\times 4\) 的矩阵,然后再将这列替换为得到的新矩阵,它们的 entry 大小都是 1 byte,使用 16 进制下的值进行运算。
每个 entry 看作 \(\operatorname{GF}(2^8)\) 下的一个多项式,有如下运算规则:
- 加法:即按位异或
- 乘法:即对应的多项式相乘,然后对 \(x^8 + x^4 + x^3 + x + 1\) 取模
AES 算法能抵御所有已公开的密码分析手段。
工作模式¶
工作模式安全性依赖于算法本身的安全性。
电子密码本模式 ECB¶
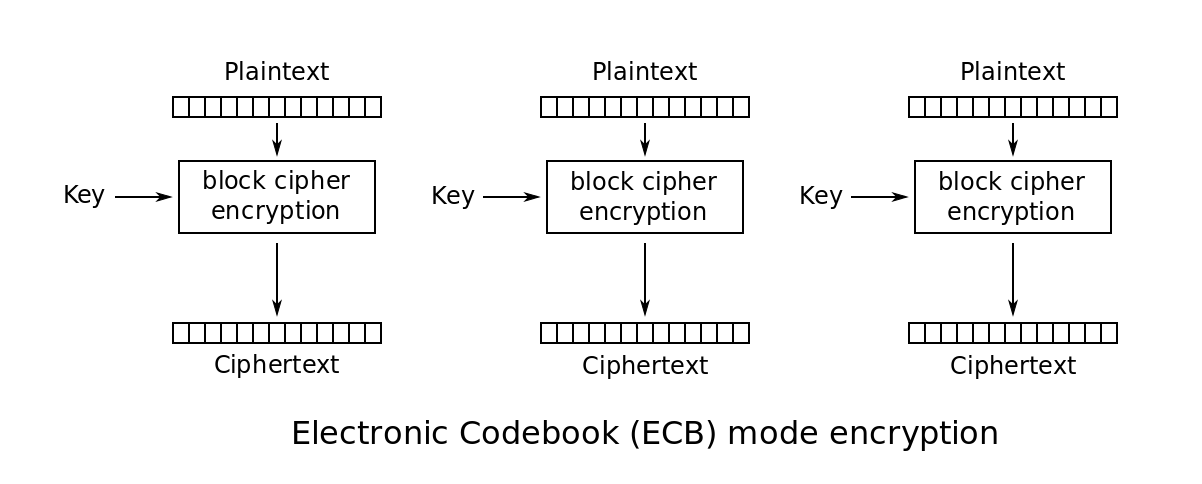
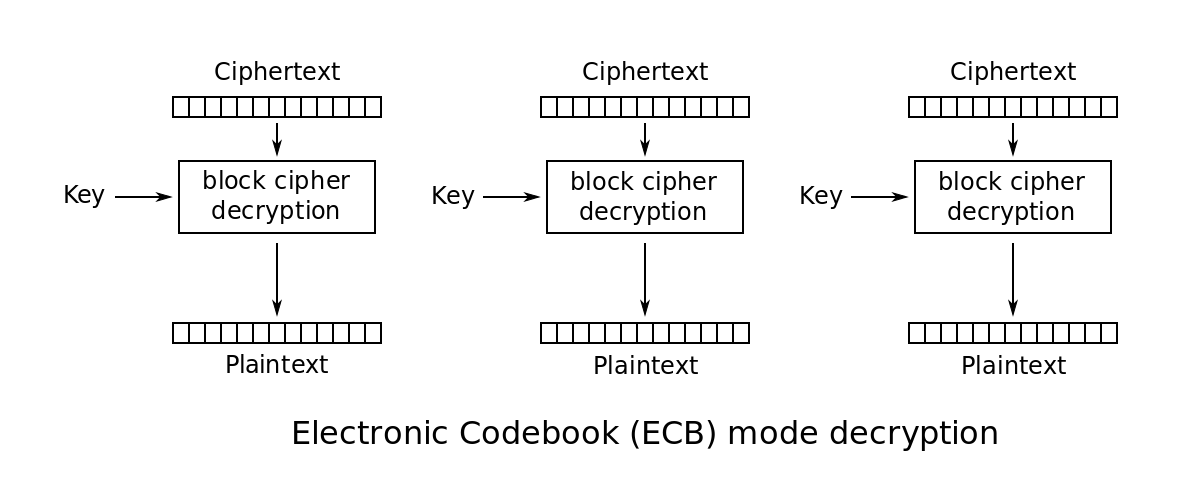
- 特点:
- 将消息分为等长的分组,对每一个分组分别用同一密钥加密
- 分组之间无任何联系
- 优点
- 简单
- 利于并行计算
- 不会传递误差
- 缺点
- 不能隐藏明文的模式,即对相同的明文分组加密会得到相同的密文分组
- 可能对明文进行主动攻击
- 适用场景:
- 传输短消息,如加密口令
密文分组链接模式 CBC¶
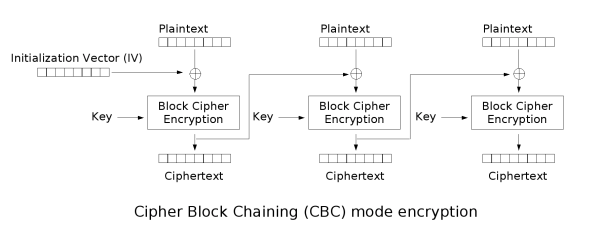
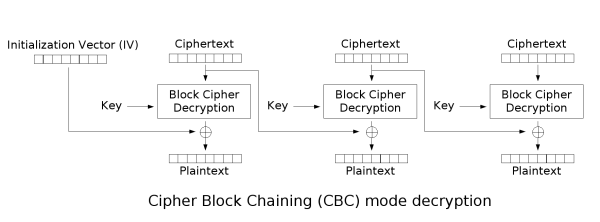
- 特点:
- 将消息分为等长的分组,对每一个分组先与前一个分组(或初始向量)异或再加密
- 分组之间相互影响
- 优点:
- 安全性好于 ECB
- 隐藏了明文模式
- 缺点:
- 误差传递
- 不利于并行计算
- 需要初始向量
- 适用场景:
- 信息认证,如消息认证码(MAC)
密文反馈模式 CFB¶
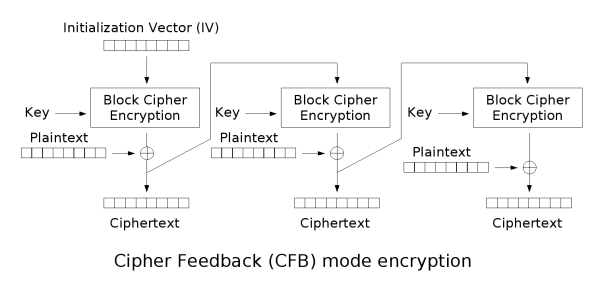

- 优点:
- 分组密码转化为流模式,可以及时加密传输小于分组的数据
- 隐藏了明文模式
- 缺点:
- 误差传递
- 不利于并行计算
- 需要初始向量
输出反馈模式 OFB¶
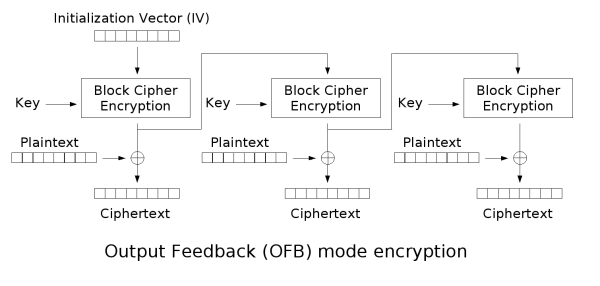
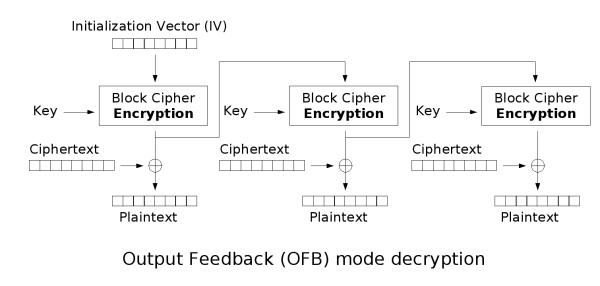
与 CFB 不同,OFB 是将上一分组得到的密钥输出进行反馈,作为下一分组密钥算法的输入。
- 优点:
- 可离线工作
- 隐藏明文模式
- 不存在误差传递,一个密文单元损坏只影响对应单元
- 缺点:
- 不利于并行计算
- 需要初始向量
- 密钥序列最终会重复
计数器模式 CTR¶
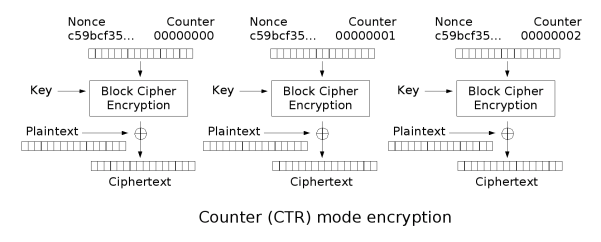
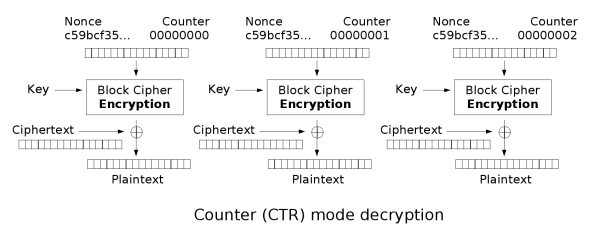
- 优点:
- 加密解密结构相同,实现简单
- 可以以任意顺序加密
- 可以并行计算
- 可证明安全
- 不存在误差传递
- 缺点:
- 密钥只能使用一次,除非能维持很长的计算器
短块处理¶
填充 Padding¶
- ANSIX923
- 最后一个字节填充填充的字节序列长度,其余填 0
- 假定块长度为 8,数据长度为 9
- 数据:
FF FF FF FF FF FF FF FF FF - 填充:
FF FF FF FF FF FF FF FF FF 00 00 00 00 00 00 07
- 数据:
- ISO10126
- 最后一个字节填充填充的字节序列长度,其余填随机数据
- 假定块长度为 8,数据长度为 9
- 数据:
FF FF FF FF FF FF FF FF FF - 填充:
FF FF FF FF FF FF FF FF FF 7D 2A 75 EF F8 EF 07
- 数据:
- PKCS7
- 每个字节填充填充的字节序列长度
- 假定块长度为 8,数据长度为 9
- 数据:
FF FF FF FF FF FF FF FF FF - 填充:
FF FF FF FF FF FF FF FF FF 07 07 07 07 07 07 07
- 数据:
- PKCS5
- 与 PKCS7 相同,但是指定块的大小为 8 bytes
- 自主指定
- None, Zeros
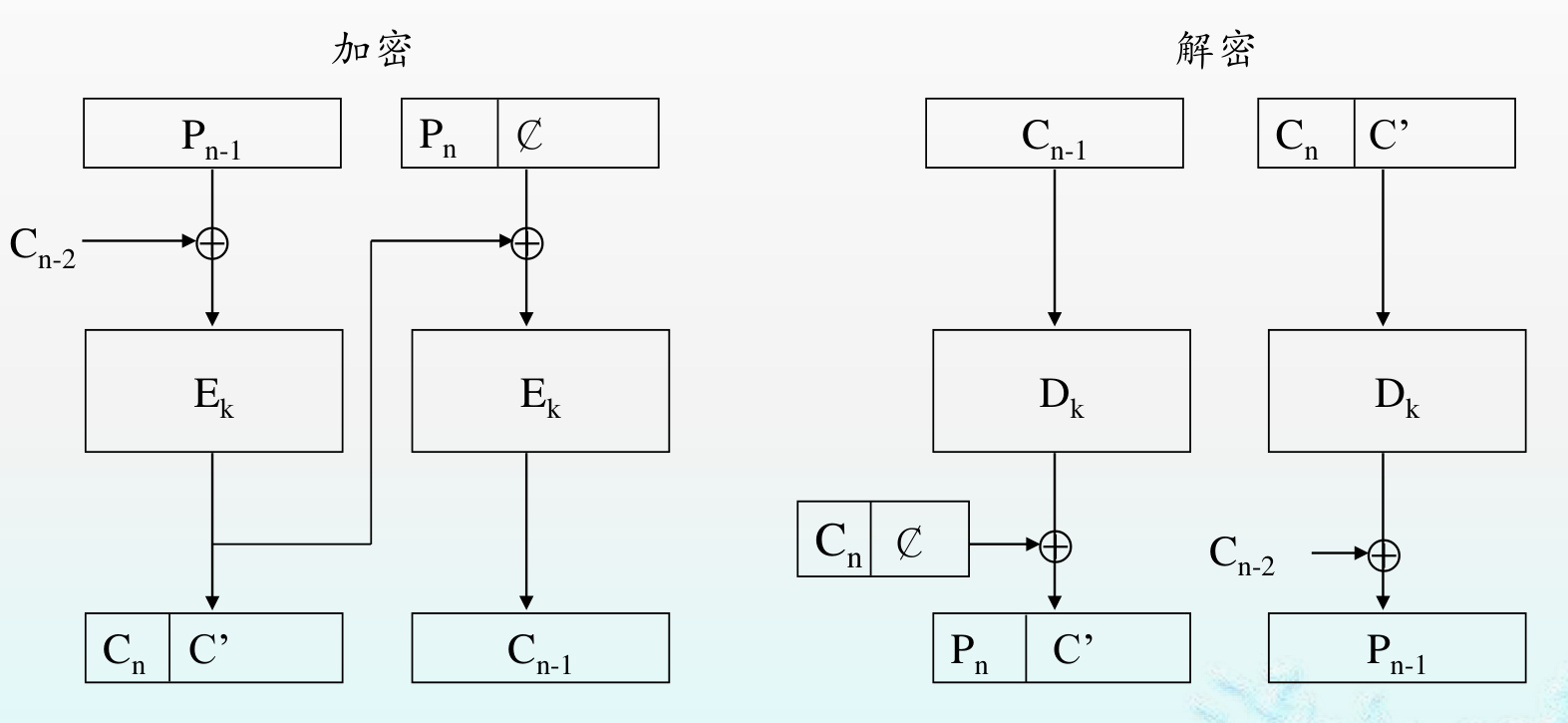
密文挪用 CTS¶
避免填充造成数据长度的扩充。
- ECB:
- CBC:
- 最后两组密文顺序调换
- 不用密文挪用
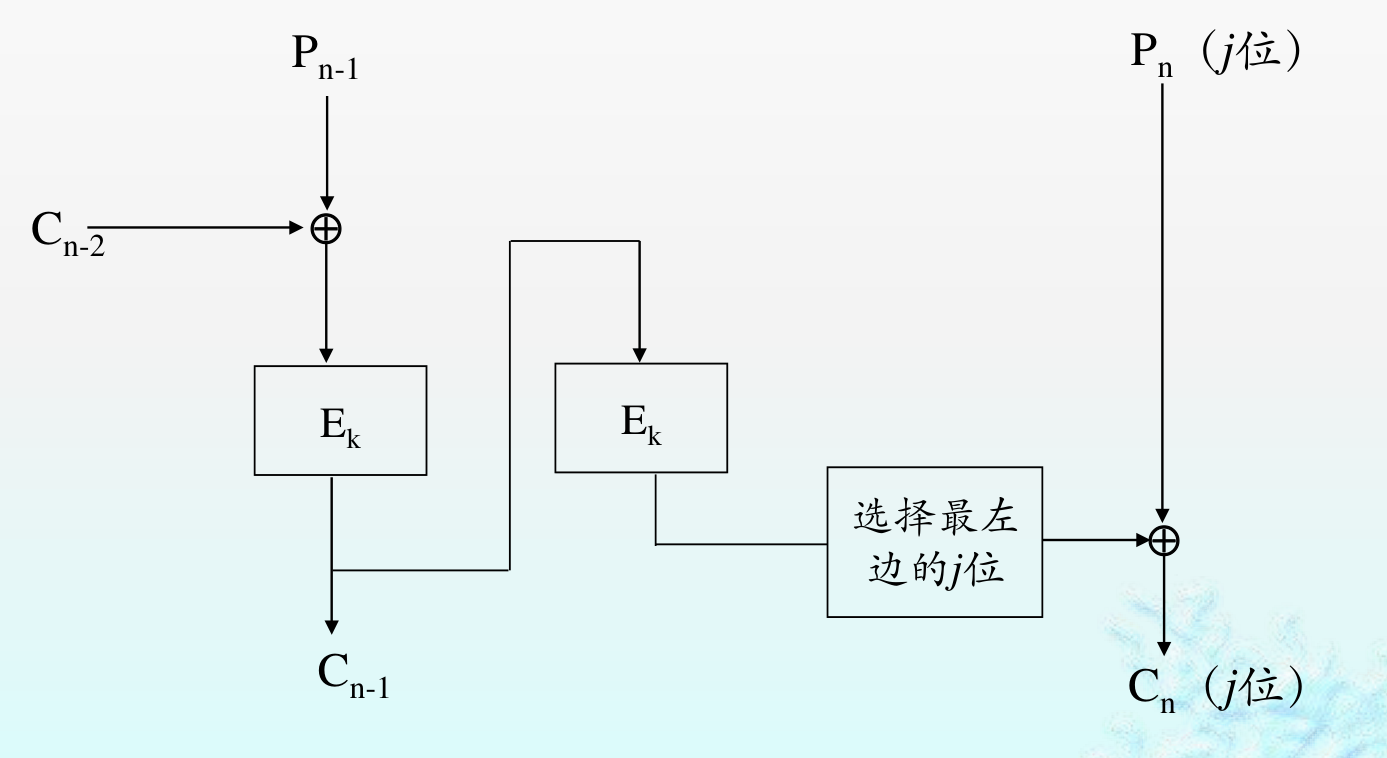
- 最后两组密文顺序调换