Skip to content

Hash 函数

信息安全的三个要点：

  • 机密性：加密技术
  • 完整性：附加冗余
    • 对称技术：Hash 函数（散列函数）、消息认证码（MAC）
    • 非对称技术：数字签名
  • 可用性：备份、灾难恢复

Hash 函数

基本要求：

  • 快速
  • 单向
  • 防碰撞

安全性：

  • 单向性（原像稳固性）：给定 \(y\)，找到 \(x\) 使得 \(h(x) = y\) 困难
    • 原像问题（攻击）：就是暴力枚举 \(X\) 中的所有元素 \(x\) 看是否满足 \(h(x) = y\)
  • 第二原像稳固性：给定 \(x\)，找到一个 \(x^\prime \in X\) 且 \(x^\prime \not= x\) 困难
    • 第二原像问题：暴力枚举 \(X/\{x\}\) 中的元素 \(x^\prime\) 看是否满足 \(h(x^\prime) = h(x)\)
  • 碰撞稳固性：找到任意满足 \(x, x^\prime \in X, x \not= x^\prime\) 且 \(h(x) = h(x^\prime)\) 的二元组 \((x, x^\prime)\) 困难
    • 碰撞问题：枚举 \(x_{0}\) ，找 \(x_{0}\) 的第二原像 \(x^\prime\)，如果找到了一对满足 \(h(x_{0}) = h(x^\prime)\) 的二元组 \((x_{0}, x^\prime)\) 就返回这个二元组，否则返回 failure

随机预言机 ROM：

  • 随机预言机是一个将所有可能输入与输出作随机映射的函数。
  • 对所有 \(x, y\) 都有 \(\Pr[h(x) = y] = \frac{1}{M}\)

Hash 函数：

  • 理想特性：混乱、扩散、随机
  • 计算速度快、不可逆
  • 通用结构：迭代结构
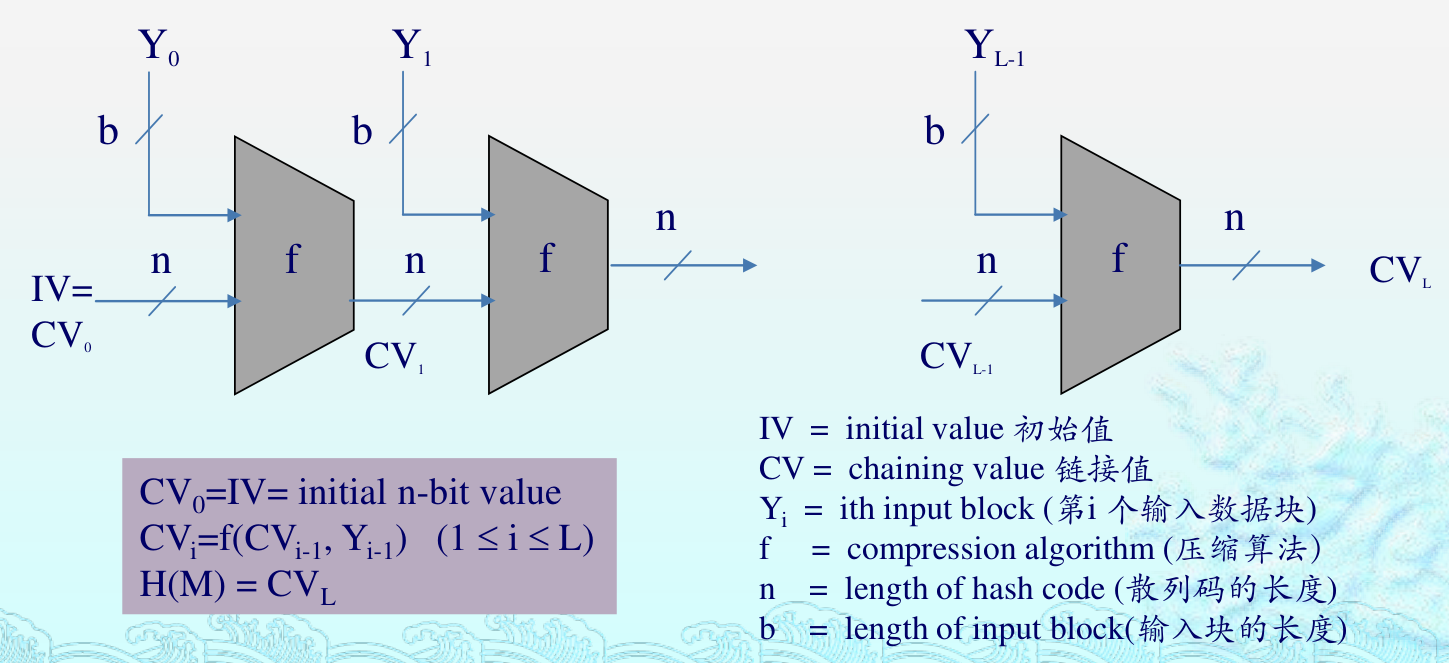
    image.png

MD5

MD5算法的C语言实现

  • 把数据分成 512 bit/块，输出 128 bit 摘要
  • 小端法，循环 64 次

SHA1

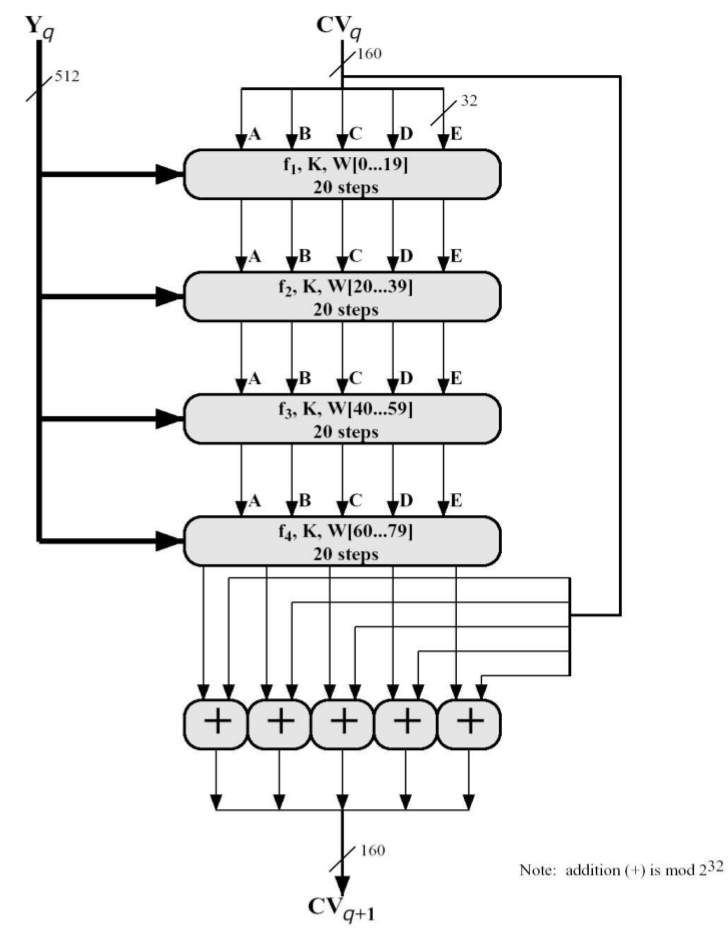
image.png

  • 要求输入消息长度 \(< 2^{64}\) ，按 512 bit/块进行分组，输出 160 bit 摘要
  • 大端存储，填充方式与 MD5 相同

与 MD5 比较：

  • 摘要长度：寻找原像和碰撞
  • 速度：SHA-1 速度慢于 MD5
  • 简洁与紧致性：描述和实现都比较简单，不需要大的代换表
  • 数据的存储方式：MD5 小端方式，SHA-1 大端方式
  • 安全性： SHA-1 优于 MD5

SM3

  • 输出 256 bit 的数据摘要，消息长度 \(< 2^{64}\) ，按 512 bit 分组
  • 过程包括填充和迭代压缩，填充方式同 MD5 和 SHA-1
  • 压缩函数使用 8 个字寄存器，大端存储，同 SHA-1，执行 64 步

SHA3

SHA-3 算法计算过程总结

  • 海绵结构
  • Keccak 算法

MAC

  • MAC 是满足某些安全性质的 Hash 函数。
  • 功能：
    • 数据完整性
    • 数据源认证
  • 构造方法：
    • 通过不带密钥的 Hash 函数构造：HMAC
    • 通过对称密码算法构造：CBC-MAC

HMAC

HMAC算法

  • \(\operatorname{HMAC}_{K}(x) = \operatorname{SHA-1}((K \oplus \operatorname{opad}) || \operatorname{SHA-1}((K \oplus \operatorname{ipad}) || x))\)
  • \(\operatorname{opad}=363636\cdots 36_{(16)}\)
  • \(\operatorname{ipad}=5C 5C 5C \cdots 5C_{(16)}\)

CBC-MAC

  • 加密算法具有混乱特性
  • 与 CBC 加密模式的区别：
    • 初始向量 IV
      • 加密模式为随机数
      • MAC 为固定的 000···000
    • 中间结果
      • 加密模式需要保存（作为密文）
      • MAC 模式不需要（仅输出最后一组密文作为摘要）
  • CCM 模式：CTR + CBC-MAC

image.png


Comments