Signals and System Properties

Signals

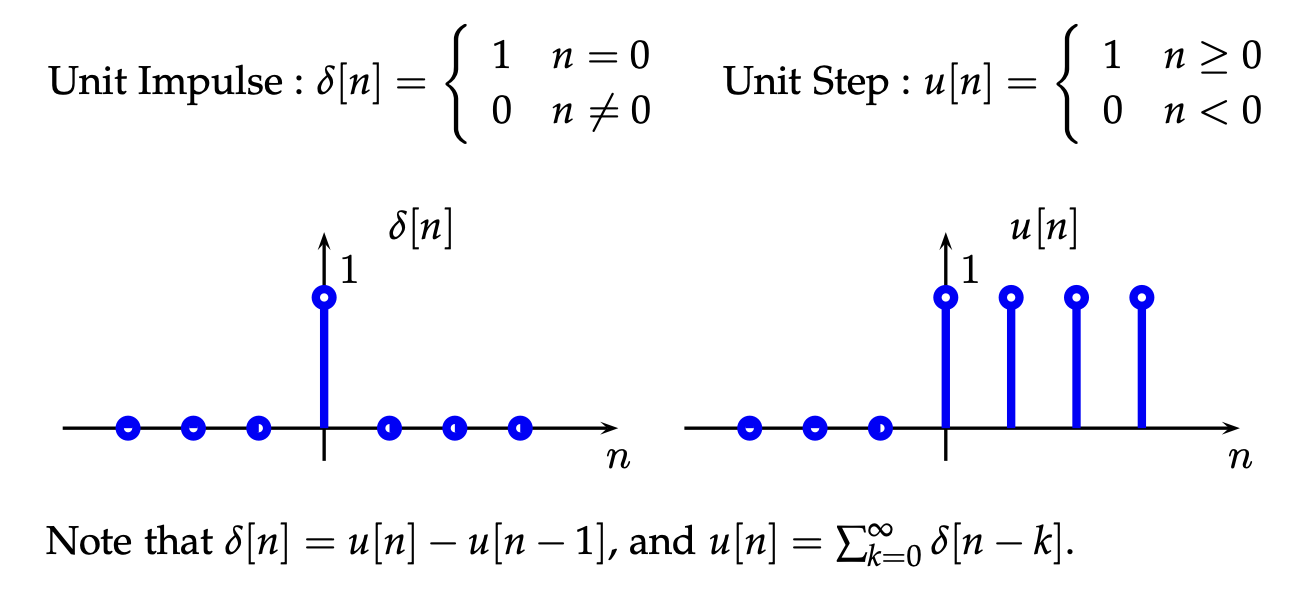
Systems

Memory

memoryless: A system is called memoryless if its output at a given time depends on the input only at that time.

Causality

causal: A system is called causal if its input depends on the input at present and past times only, not on future times.

Stability

stable: A system is stable if all bounded inputs generate bounded outputs.

Linearity

linear: A system is called linear if it satisfies these two conditions

1. Scaling: \(ax(t) \to ay(t)\)
2. Superposition: \(x_1(t) + x_2(t) \to y_1(t) + y_2(t)\)

Corollary

If the input to a linear system is 0, the output must be 0.

Time-Invariance

time-invariant: A system is called time-invariant if a time shift in the input results is an identical time shift in the output:

\[ x(t-T) \to y(t-T) \]

for any input-output pair and any amount of shift \(T\).

LTI Systems and Convolution

LTI systems 是强大的 analysis tools，尤其是在已知它对 unit impulse 的 response 后我们可以预测给定 input 在任意时刻的 response

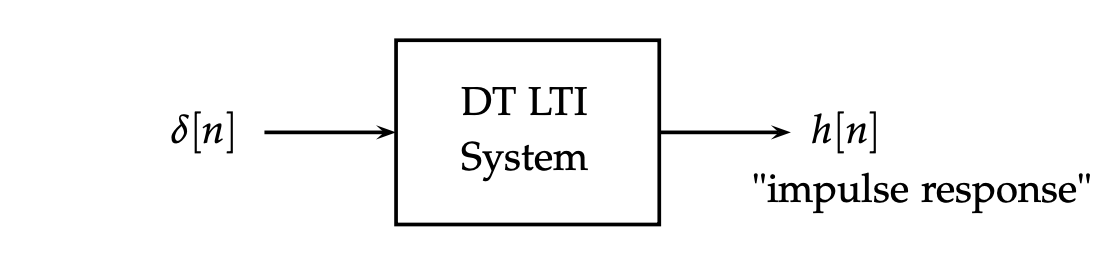
为了得到 \(x[n]\) 的 response，我们将其用 \(\delta[n]\) 来表示，即：

\[ x[n] = \dots + x[-1]\delta[n+1] + x[0]\delta[n] + x[1]\delta[n-1] + \dots \]

由 time-invariance，有 \(\delta[n-k]\to h[n-k]\) ，再由 linearity，有

\[ y[n] = dots + x[-1]h[n+1] + x[0]h[n] + x[1]h[n-1] + \dots \]

即给定 input \(x[n]\)，有 output

\[ y[n] = \sum^{\infty}_{k=-\infty} x[k]h[n-k] \]

定义右边为卷积运算，即

\[ (x \ast h)[n] \coloneqq \sum_{k=-\infty}^{\infty} x[k]h[n-k] \]

red pink purple deep purple indigo blue light blue cyan teal green light green lime yellow amber orange deep orange brown grey blue grey black white

Comments