Skip to content

Linear Algebra Done Wrong

Info

「Linear Algebra Done Wrong」by Sergei Treil

Warning

本文写得很随意 qwq

Systems of Linear Euqations

image.png

从信息量的角度来理解：

无论是从 row vectors 形成的空间还是 column vectors 形成的空间来看，他们所有给出的信息都可以用同一个 matrix 来概括，也就是信息量是相等的，那么他们所形成的 space 必然也会是相同的。

也就是说，他们的 space 取决于维度较小者，假如 # row > # col，那么 column vectors 多出来的维度没有传达任何信息，于是这个 matrix 一定会存在冗余信息，此时表现在 row vectors 上就是多余的 vectors。

Quote

这种更感性的理解往往是发现新领域、新方法的突破口，纯粹的数字推演更多的是在发现后证明其思路严谨性的工具。

——没错，是我说的😎

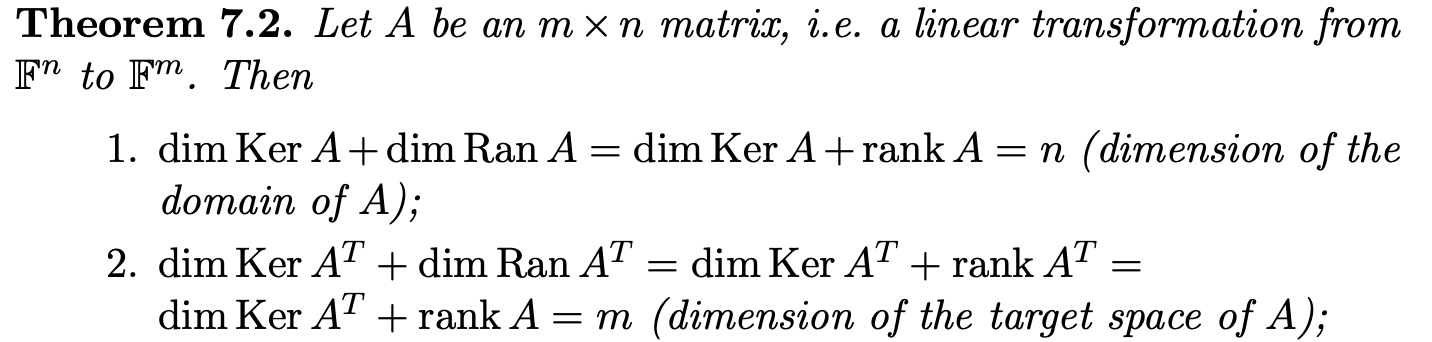
Screenshot 2024-02-20 at 17.27.16.png

\(\dim{\mathrm{Ker}\, A}\rightarrow\) # free variables of \(A_e\) , \(\dim{\mathrm{Ran}\, A} \rightarrow\) # pivots of \(A_e\)

# free variables + # pivots = # col of \(A_e\) = # col of \(A\) = \(n\)

给定线性无关的向量组 \(\vec{v_1}, \vec{v_2}, \dots, \vec{v_r}\)，求出需要添加的向量 \(\vec{v_{r+1}}, \dots, \vec{v_{n}}\) 使其成为 space \(V\) 的一组 basis。

将 \(\vec{v_1}, \vec{v_2}, \dots, \vec{v_r}\) 写成矩阵 \(A\) 的 row vectors，然后求出 \(A_e\) ，在 \(A_e\) 中添加缺失的 row vector 使其成为 \(n\times n\) 的 invertible matrix，添加的这些 row vectors 就是 \(\vec{v_{r+1}}, \dots, \vec{v_{n}}\)。

Screenshot 2024-02-27 at 20.45.33.png

\([T]_{\mathcal{BA}}\) 的第 \(k\) 列等于 \([T\vec{a_k}]_{\mathcal{B}}\) :

\[ \begin{aligned} B[T\vec{v}]_{\mathcal{B}}&=T\vec{v}=TA[\vec{v}]_{\mathcal{A}}\\ \therefore[T\vec{v}]_{\mathcal{B}}&=B^{-1}TA[\vec{v}]_{\mathcal{A}}=[TA]_{\mathcal{B}}[\vec{v}]_{\mathcal{A}} \end{aligned} \]

当 \(T=I\) 时，有 \([I]_{\mathcal{BA}}=[A]_{\mathcal{B}}\)，并且 \([I]^{-1}_{\mathcal{BA}}=[I]_{\mathcal{AB}}\)

对于 standard basis \(\mathcal{S}\)，有 \([I]_{\mathcal{SB}}=B\)，\([I]_{\mathcal{BS}}=B^{-1}\)，在上面的推导中其实隐含了 \(\vec{v}\) 是 \(\mathcal{S}\) 下的坐标。

不难得到

\[ [T]_{\mathcal{BB}} = [I]_{\mathcal{BA}}[T]_{\mathcal{AA}}[I]_{\mathcal{AB}}=[I]_{\mathcal{AB}}^{-1}[T]_{\mathcal{AA}}[I]_{\mathcal{AB}} \]

令 \(Q=[I]_{\mathcal{AB}}\)，于是有

\[ [T]_{\mathcal{BB}} = Q^{-1}[T]_{\mathcal{AA}}Q \]

Determinants

将矩阵看成 column vectors 的组合，首先考虑 \(2\times 2\) 的矩阵，那么它的 volume 就是两个向量组成的平行四边形的面积，如果是 \(3\times 3\) 的矩阵，则是它们组成的立方体的体积，如果是 \(n\times n\) 的矩阵呢？我们定义它的 volume 是 \(D(\vec{v_1}, \dots, \vec{v_n})\) ，也可以写作 \(\det A\) ，从这个角度来看，一下几个性质就很显然了：

  1. \(D(\alpha\vec{v_1}, \dots, \vec{v_n})=\alpha D(\vec{v_1}, \dots, \vec{v_n})\)
  2. \(D(\vec{v_1}, \dots, \vec{u_k}+\vec{v_k}, \dots, \vec{v_n})=D(\vec{v_1}, \dots, \vec{u_k}, \dots, \vec{v_n})+D(\vec{v_1}, \dots, \vec{v_k}, \dots, \vec{v_n})\)

可以发现，我们对矩阵 \(A\) 做 row operations，对于 \(|A|\) 的影响只是前面的系数，根据前面 invertible 的知识，我们可以得出 A is invertible \(\iff\) \(|A| \not= 0\)

Lemma

Any invertible matrix is a product of elementary matrices.

由以上 lemma 我们也不难得出以下结论：

  1. \(\det{A} = \det{A^T}\)
  2. \(\det{(AB)}=(\det{A})(\det{B})\)

对 determinant 的实际意义有了一个基本的概念后，我们需要给它下一个 formal definition，于是便有了国内大部分教材引入行列式的概念时用到的基于逆序对和排列的定义，具体推导过程可以看书，不再赘述。

在这之后，作者介绍了 determinant 写成 entries 与 cofactors 的线性组合的形式，这种形式是用来计算维度较大的行列式的主要方法。

Theorem

Let \(A\) be an invertible matrix and let \(C\) be its cofactor matrix.

Then
\(\(A^{-1} = \dfrac{1}{\det{A}}C^T\)\)

再由方程组的矩阵形式 \(\mathrm{Ax=b}\) 我们可以引出 Cramer's rule.

Cramer's rule

For an invertible matrix \(A\) the entry number \(k\) of the solution of the equation \(\mathrm{Ax = b}\) is given by the formula
$$ x_k = \dfrac{\det{B_k}}{\det{A}} $$
where the matrix \(B_k\) is obtained from \(A\) by replacing column number \(k\) of \(A\) by the vector \(\mathrm{b}\).


Comments