The geometry of linear programming

Polyhedra and convex sets

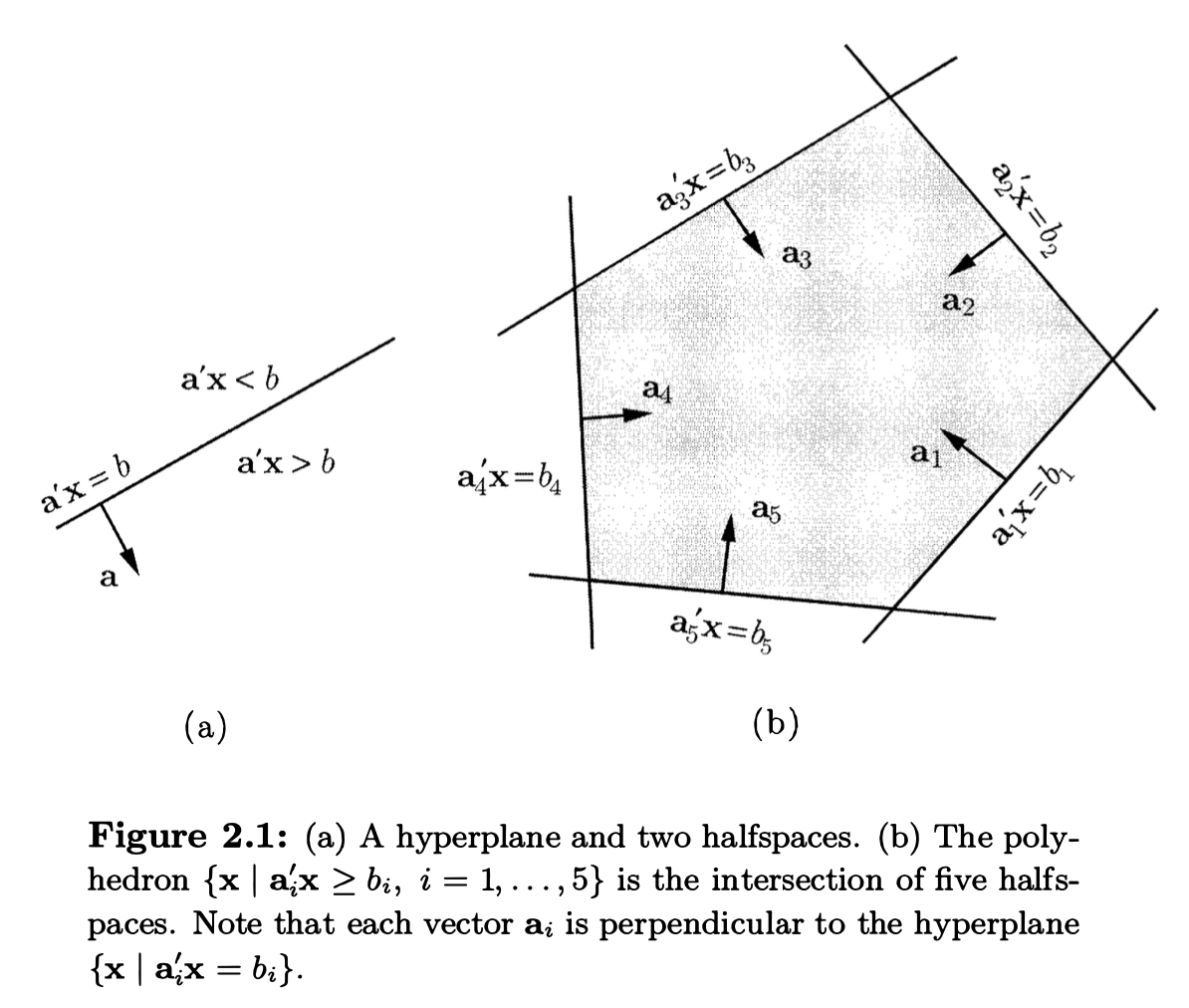
Hyperplanes, halfspaces, and polyhedra

Polyhedron

A polyhedron is a set that can be described in the form \(\{\mathbf{x}\in \mathfrak{R}^n | \mathbf{Ax \geq b}\}\), where \(\mathbf{A}\) is an \(m \times n\) matrix and \(\mathbf{b}\) is a vector in \(\mathfrak{R}^m\) .

根据 LP 的 general form, 任何 LP prob 的 feasible sets 都是 polyhedron. 形如 \(\{\mathbf{x} \in \mathfrak{R}^n | \mathbf{Ax=b, x\geq{0}}\}\) 的 set 也会是一个 polyhedron, 我们称之为 polyhedron in standard form.

Definition

A set \(S \subset \mathfrak{R}^n\) is bounded if there exists a constant \(K\) that the absolute value of every component of every element of \(S\) is less than or equal to \(K\).

hyperplane 与 halfspace 是与 single linear constraint 相关的概念.

Hyperplane/Halfspace

Let \(\mathbf{a}\) be a nonzero vector in \(\mathfrak{R}^n\) and let \(b\) be a scalar.

1. The set \(\{\mathbf{x}\in \mathfrak{R}^n | \mathbf{a'x}= b\}\) is called a hyperplane.
2. The set \(\{\mathbf{x} \in \mathfrak{R}^n | \mathbf{a'x}\geq b\}\) is called a halfspace.

Note

hyperplane 是 halfspace 的边界.
另外, \(\mathbf{a}\) 与 hyperplane 是 perpendicular 的关系.
一个 polyhedron 是有限个 halfspaces 的 intersection.

Convex Sets

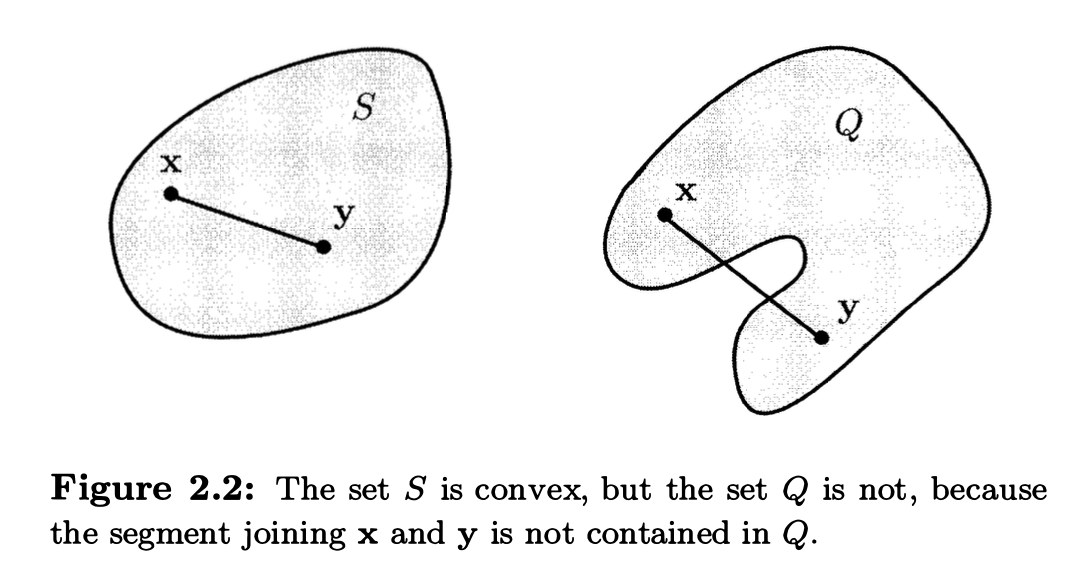
Convex sets

A set \(S \subset \mathfrak{R}^n\) is convex if for any \(\mathbf{x, y} \in S\), and any \(\lambda \in [0, 1]\), we have \(\lambda \mathbf{x} + (1-\lambda)\mathbf{y} \in S\).

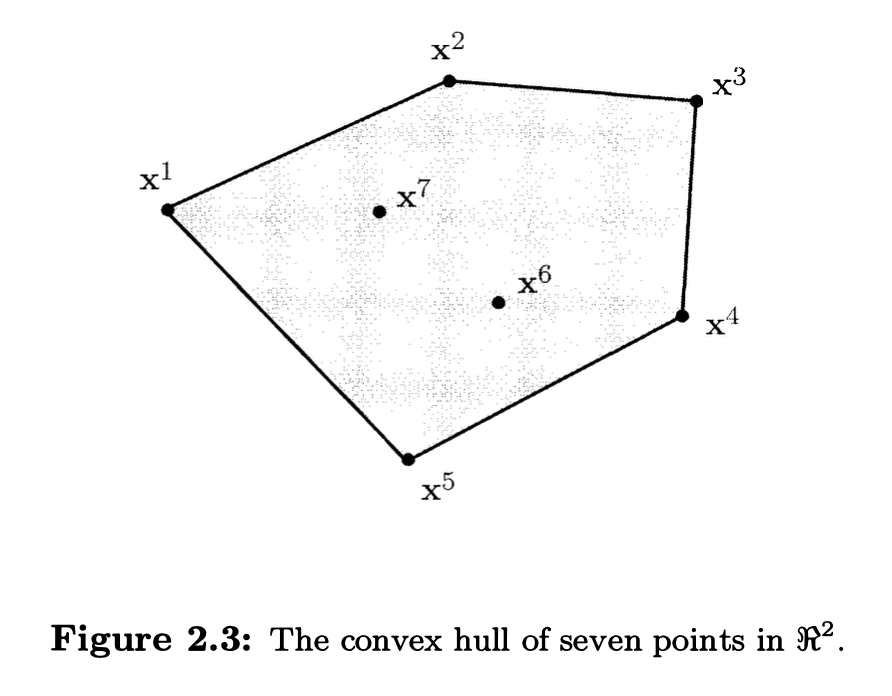
Convex combination/hull

Let \(\mathbf{x}^1, \dots, \mathbf{x}^k\) be vectors in \(\mathfrak{R}^n\) and let \(\lambda_{1}, \dots, \lambda_{k}\) be nonnegative scalars whose sum is unity.

1. The vector \(\sum_{i=1}^k \lambda_{i}\mathbf{x}^i\) is said to be a convex combination of the vectors \(\mathbf{x}^1, \dots, \mathbf{x}^k\).
2. The convex hull of the vectors \(\mathbf{x}^1, \dots, \mathbf{x}^k\) is the set of all convex combinations of these vectors.

下面的定理阐述了上面提到的几个概念之间的关系.

Theorem

1. The intersection of convex sets is convex.
2. Every polyhedron is a convex set.
3. A convex combination of a finite number of elements of a convex set also belongs to that set.
4. The convex hull of a finite number of vectors is a convex set.

Extreme points, vertices, and basic feasible solutions

在 Section 1.4 中可以看出, 最优解倾向于出现在 polyhedron 的 “corner” 中. 本节会用 3 种不同方式定义 “corner”, 然后解释这三种定义之间是等价的.

Extreme point

Let \(P\) be a polyhedron. A vector \(\mathbf{x} \in P\) is an extreme point of \(P\) if we cannot find two vectors \(\mathbf{y}, \mathbf{z} \in P\), both different from \(\mathbf{x}\), and a scalar \(\lambda \in [0,1]\), such that \(\mathbf{x}=\lambda \mathbf{y} + (1-\lambda) \mathbf{z}\).

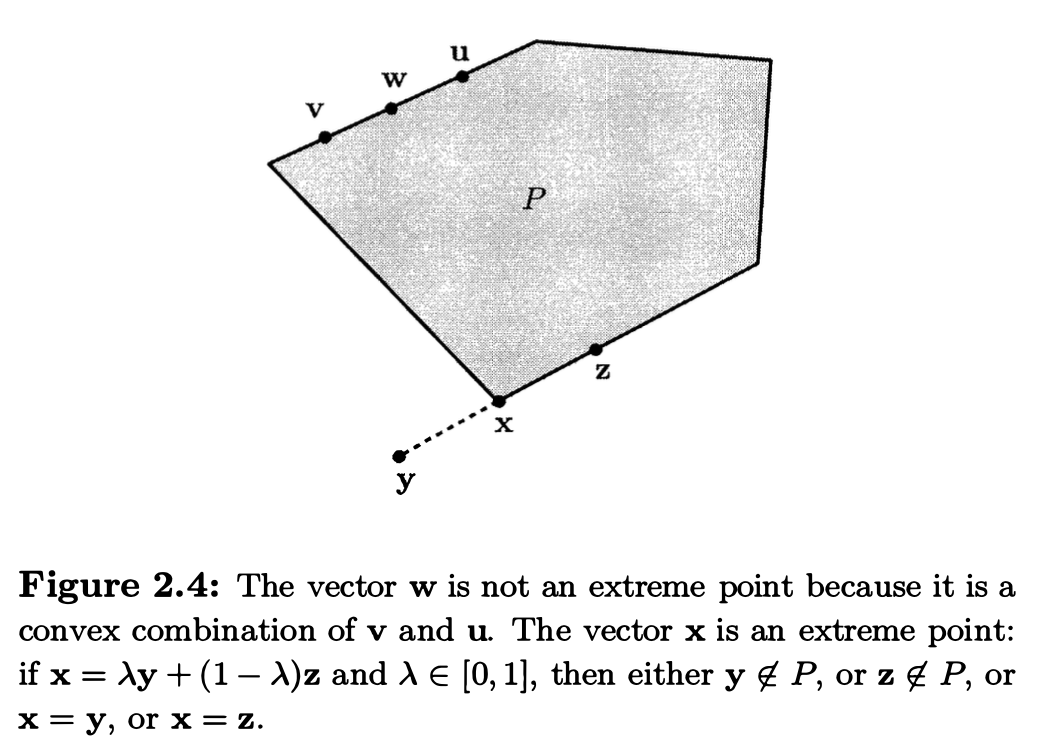
extreme point 就是不能被 \(P\) 中其他任意两个点的 convex combination 表示的点.

Vertex

Let \(P\) be a polyhedron. A vector \(\mathbf{x} \in P\) is a vertex of \(P\) if there exists some \(\mathbf{c}\) such that \(\mathbf{c'x} < \mathbf{c'y}\) for all \(\mathbf{y}\) satisfying \(\mathbf{y} \in P\) and \(\mathbf{y} \not= \mathbf{x}\).

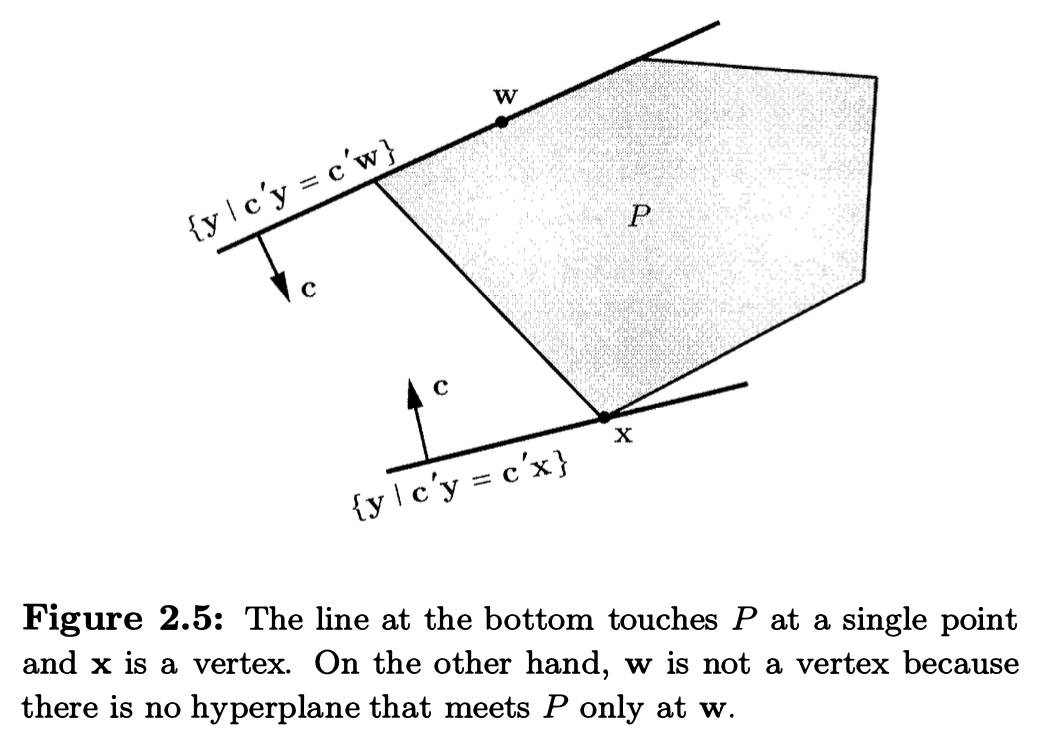
vertex 就是我们能找到一个 hyperplane \(\{\mathbf{y} | \mathbf{c'y}=\mathbf{c'x}\}\) 使得 \(P\) 在这个 hyperplane 的一侧且与这个 hyperplane 有且仅有一个交点 \(\mathbf{x}\), 这个 \(\mathbf{x}\) 就是 vertex.

下面给出一个用 linear constraints 表示的, 并且能导出为 algebraic test 的 definition.

考虑用以下 linear equality and inequality constraints 定义的 polyhedron \(P \subset \mathfrak{R}^n\)

\[\begin{aligned}&\mathrm{a}_{i}^{\prime}\mathrm{x~\geq~}b_{i},\quad&i\in M_{1},\\&\mathrm{a}_{i}^{\prime}\mathrm{x~\leq~}b_{i},\quad&i\in M_{2},\\&\mathrm{a}_{i}^{\prime}\mathrm{x~=~}b_{i},\quad&i\in M_{3},\end{aligned}\]

其中 \(M_{1}, M_{2}, M_{3}\) 为 finite index sets, \(\mathbf{a}_{i}\) 是 \(\mathfrak{R}^n\) 中的 vector, \(b_{i}\) 是 scalar.

Active/Binding

If a vector \(\mathbf{x}^*\) satisfies \(\mathbf{a}_{i}'\mathbf{x}^* = b_{i}\) for some \(i\) in \(M_{1}, M_{2},\) or \(M_{3}\), we say that the corresponding constraint is active or binding at \(\mathbf{x}^*\).

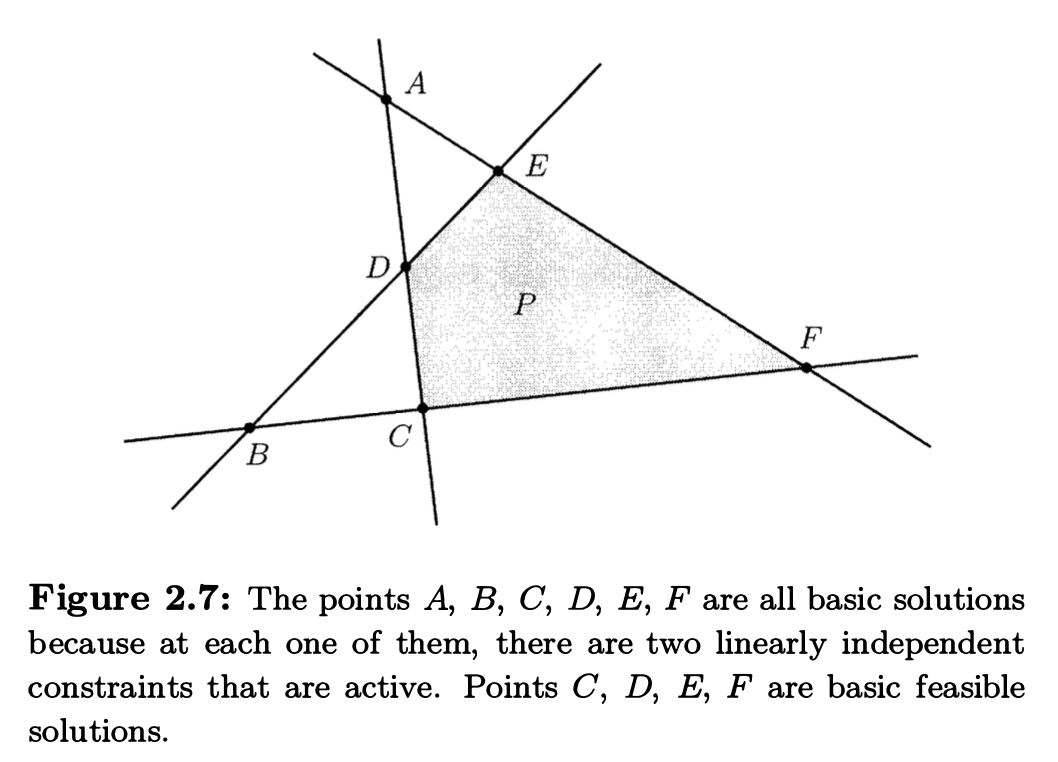
当满足在 \(\mathbf{x}^*\) 处 active 的 constraints 有 \(n\) 个时, 我们则得到了一个 \(n\) linear equations in \(n\) unknowns. 当且仅当这 \(n\) 个 equations 是 “linear independent” 时这个系统有唯一解.

Theorem

Let \(\mathbf{x}^*\) be an element on \(\mathfrak{R}^n\) and let \(I = \{i | \mathbf{a}_{i}'\mathbf{x}^* = b_{i}\}\) be the set of indices of constraints that are active at \(\mathbf{x}^*\). Then, the following are equivalent:

1. There exist \(n\) vectors in the set \(\{\mathbf{a}_{i} | i \in I\}\), which are linearly independent.
2. The span of the vectors \(\mathbf{a}_{i}\), \(i \in I\), is all of \(\mathfrak{R}^n\), that is, every element of \(\mathfrak{R}^n\) can be expressed as a linear combination of the vectors \(\mathbf{a}_{i}\), \(i \in I\).
3. The system of equations \(\mathbf{a}_{i}' \mathbf{x} = b_{i}\), \(i \in I\), has a unique solution.

换句话说, 当我们拥有了 \(n\) 个 linearly independent active constraints 时, 就可以得到一个 unique vector \(\mathbf{x}^*\). 不过, \(\mathbf{x}^*\) 不一定能满足 inactive constraints, 此时若它能满足所有的 equality constraints 我们就称 \(\mathbf{x}^*\) 是一个 basic solution.

Basic (feasible) solution

Consider a polyhedron \(P\) defined by linear equality and inequality constraints, and let \(\mathbf{x}^*\) be an element of \(\mathfrak{R}^n\).

1. The vector \(\mathbf{x}^*\) is a basic solution if:
   1. All equality constraints are active;
   2. Out of the constraints that are active at \(\mathbf{x}^*\), there are \(n\) of them that are linearly independent.
2. If \(\mathbf{x}^*\) is a basic solution that satisfies all of the constraints, we say that it is a basic feasible solution.

到目前为止, 我们给出了 3 个针对同一个概念的不同定义, 其中 2 个是 geometric (extreme point, vertex), 另一个是 algebraic (basic feasible solution).

Theorem

Let \(P\) be a nonempty polyhedron and let \(\mathbf{x}^* \in P\). Then, the following are equivalent:

1. \(\mathbf{x}^*\) is a vertex;
2. \(\mathbf{x}^*\) is an extreme point;
3. \(\mathbf{x}^*\) is a basic feasible solution.

Proof

vertex \(\implies\) extreme point:

因为 \(\mathbf{x}^*\) 是 vertex, 因此存在 \(\mathbf{c}\) 使得 \(\mathbf{c'x}\) 在 \(\mathbf{x}^*\) 处取得最小值. 若 \(\mathbf{x}^*\) 不是 extreme point, 于是 \(\exists \mathbf{y}, \mathbf{z} \in P, \lambda \in [0, 1], s.t. \mathbf{x}^* = \lambda \mathbf{y} + (1-\lambda)\mathbf{z}\). 此时有

\[\begin{aligned}\mathbf{c'x} &= \lambda \mathbf{c'y} + (1-\lambda)\mathbf{c'z}\\ &> λ \mathbf{c'x}^* + (1-λ) \mathbf{c'x}^* = \mathbf{c'x^*}\end{aligned}\]

矛盾, 因此 \(\mathbf{x}^*\) 是 extreme point.

basic feasible solution \(\implies\) vertex:

由 \(\mathbf{x}^*\) 是 basic feasible solution, 我们可以找到 \(n\) 个线性无关的约束 \(\mathbf{a}_{i} \in \mathfrak{R}^n\) 以及它们对应的 \(b_{i}\), 满足 \(\mathbf{a}'_{i}\mathbf{x}^* = b_{i}\), 设这样的 \(n\) 个约束下标集合为 \(I\). 不失一般性地, 我们令 \(P\) 为 general form polyhedron, 从而任取 \(\mathbf{x} \in P, \mathbf{x}\not= \mathbf{x}^*\), 都有 \(\mathbf{a}_{i}'\mathbf{x} \geq b_{i}, \forall i \in I\).

因为 \(\mathbf{a}_{i}, \forall i \in I\) 线性无关, 因此线性方程组 \(\mathbf{a}_{i}'\mathbf{x} = b_{i}, \forall i \in I\) 有唯一解 \(\mathbf{x}^*\). 令 \(\mathbf{c} = \sum_{i \in I}\mathbf{a}_{i}\), 则 \(\mathbf{c}'\mathbf{x}^* = \sum_{i \in I}b_{i}\). 任取 \(\mathbf{x} \in P, \mathbf{x} \not= \mathbf{x}^*\), 我们有

\[\mathbf{c}'\mathbf{x} = \sum_{i \in I}\mathbf{a}_{i}'\mathbf{x} \geq \sum_{i \in I}b_{i} = \mathbf{c}'\mathbf{x}^*\]

当且仅当 \(\mathbf{x}\) 为满足线性方程组 \(\mathbf{a}_{i}'\mathbf{x} = b_{i}, \forall i \in I\) 时取等, 因为 \(\mathbf{x} \not= \mathbf{x}^*\), 所以无法取到等号, 从而 \(\mathbf{c}'\mathbf{x} > \mathbf{c}'\mathbf{x}^*\), 因此 \(\mathbf{x}^*\) 是 vertex.

extreme point \(\implies\) basic feasible solution:

考虑证明逆否命题. 设 \(\mathbf{x}^*\) 不是 basic solution, 则至多有 \(m < n\) 个线性无关的 constraints 能在 \(\mathbf{x}^*\) 处 active, 设它们的序号集合为 \(I\), 其余 inactive at \(\mathbf{x}^*\) 的 constraints 的集合记作 \(I'\). 不妨令 \(P\) 为 general form polyhedron.

在 \(\mathfrak{R}^n\) 中我们至少能找到一个 \(\mathbf{d}\) 使得 \(\mathbf{a}_{i}'\mathbf{d} = 0, \forall i \in I\). 任取一个满足条件的 \(\mathbf{d}\), 我们总能找到一个足够小的 \(\epsilon>0\), 然后令 \(\mathbf{y}=\mathbf{x}^* + \epsilon \mathbf{d}, \mathbf{z} = \mathbf{x}^* - \epsilon\mathbf{d}\), 此时有 \(\mathbf{a}_{i}'\mathbf{y}=\mathbf{a}_{i}'\mathbf{z}=b_{i}, \forall i \in I\) 且 \(\mathbf{a}_{i}'\mathbf{y} > b_{i}, \mathbf{a}_{i}'\mathbf{z} > b_{i}, \forall i \in I'\), 从而 \(\mathbf{y}, \mathbf{z} \in P\), 又 \(\mathbf{x}^* = \frac{1}{2}\mathbf{y}+\frac{1}{2}\mathbf{z}\), 因此 \(x^*\) 不是 extreme point, 逆否命题得证, 从而原命题得证.

综上, 所证定理的三个命题等价.

Corollary

Given a finite number of linear inequality constraints, there can only be a finite number of basic or basic feasible solutions.

Proof

给一个不太严谨的证明.

假设给出了 \(m\) 个 linear inequality constraints, 从其中取出 \(n\) 个满足 linearly independent constraints 的取法是有限的, 而每个取法都唯一对应一个 basic (feasible) solution, 因此 basic (feasible) solution 的数量也一定是有限的.

Polyhedra in standard form

考虑 standard form 的 LP, 令 \(P = \{\mathbf{x} \in \mathfrak{R}^n | \mathbf{Ax} = \mathbf{b}, \mathbf{x} \geq \mathbf{0}\}\), 我们希望找到 basic solution. 不妨设 \(\mathbf{A}\) 是一个 \(m \times n\) 的矩阵且这 \(m\) 个 row vectors 是 linearly independent 的, \(\mathbf{x}\) 要有解的话必然有 \(m \leq n\). 显然解出 \(\mathbf{Ax} = \mathbf{b}\) 只能有 \(m\) 个 active constraints, 此时我们只需要将剩下 \(n-m\) 个 \(x_{i}\) 设为 \(0\) 来满足 \(\mathbf{x} \geq 0\) 即可得到 \(n\) 个 active constraints.

Theorem

Consider the constraints \(\mathbf{Ax} = \mathbf{b}\) and \(\mathbf{x} \geq \mathbf{0}\) and as­sume that the \(m \times n\) matrix \(\mathbf{A}\) has linearly independent rows. A vector \(x \in \mathfrak{R}^n\) is a basic solution if and only if we have \(\mathbf{Ax} = \mathbf{b}\), and there exist indices \(B(1), \dots, B(m)\) such that:

1. The columns \(\mathbf{A}_{B(1)}, \dots, \mathbf{A}_{B(m)}\) are linearly independent;
2. If \(i \not= B(1), \dots, B(m)\), then \(x_{i}=0\).

通过上述定理, 我们可以根据下面的程序来构造出一个 standard form polyhedron 的所有 basic solutions.

Procedure for constructing basic solutions

1. Choose \(m\) linearly independent columns \(\mathbf{A}_{B(1)}, \dots, \mathbf{A}_{B(m)}\).
2. Let \(x_{i}=0\) for all \(i \not= B(1), \dots, B(m)\).
3. Solve the system of \(m\) equations \(\mathbf{Ax} = \mathbf{b}\) for the unknowns \(x_{B(1)}, \dots, x_{B(m)}\).

如果通过这个程序得到的一个 basic solution 满足 nonnegative, 那么它就是一个 basic feasible solution.

若 \(\mathbf{x}\) 是一个 basic solution, 那它对应的 \(x_{B(1)}, \dots, x_{B(m)}\) 被称为 basic variables, 其余的 variables 则称为 nonbasic, 同理, 对应的 columns \(\mathbf{A}_{B(1)}, \dots, \mathbf{A}_{B(m)}\) 为 basic columns, 并且它们 form a basis of \(\mathfrak{R}^m\). 对于 \(\mathbf{A}\) 的 basic columns 有不同组合, 也就会得到 distinct/different bases; 我们通常将 basic indices 集合 \(\{B(1), \dots, B(m)\}\) 不同的 bases 看作是不同的. (翻译的有点绕口 QAQ)

由 \(m\) 个 basic columns 组合而成的 matrix \(\mathbf{B}\) 称为 basic matrix, 类似地我们也可以定义 basic variables 的组合 vector \(\mathbf{x}_{B}\).

借由下图可以得到一个 intuitive view of basic solutions.

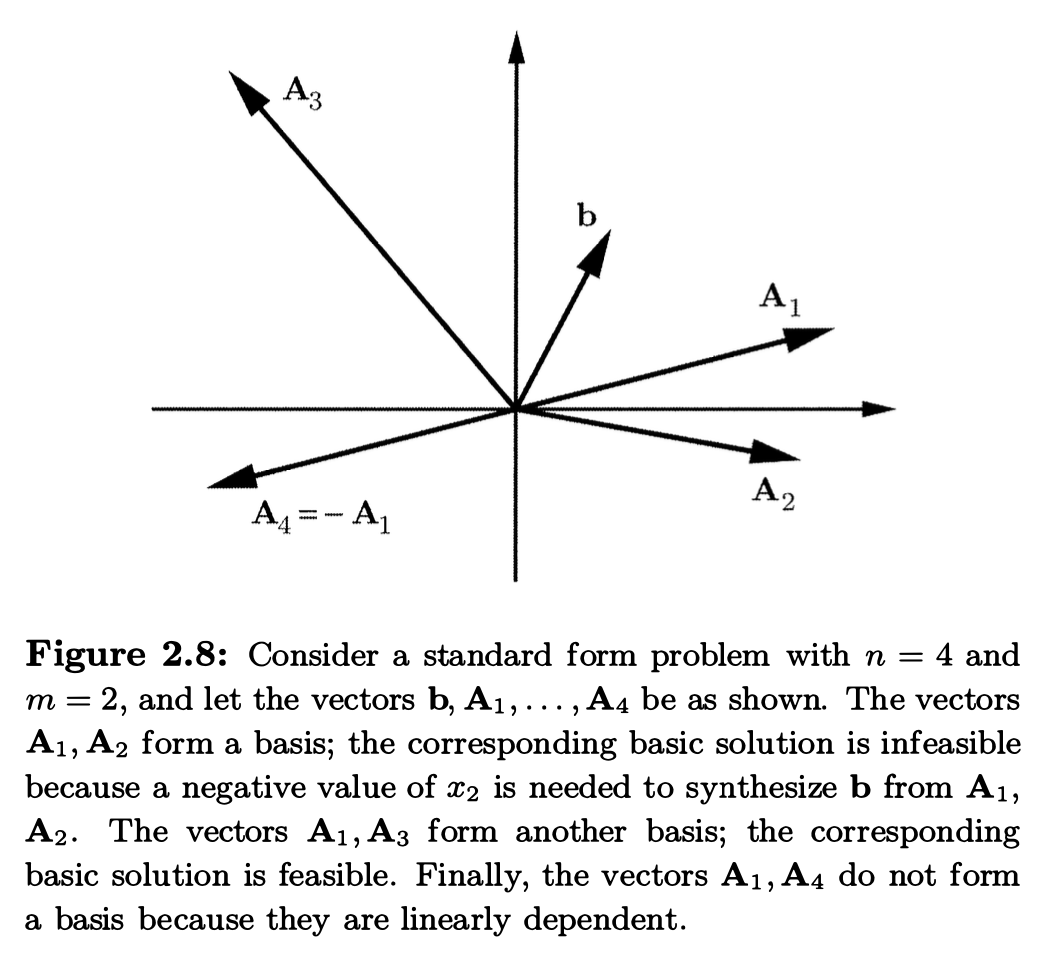
Correspondence of bases and basic solutions

bases 到 basic solution 的映射关系可以看作一个非单射函数, 即不同的 bases 可能得到相同的 basic solution, 这一现象有重要的 algorithmic implications, 与 degeneracy 密切相关.

Adjacent basic solutions and adjacent bases

当两个不同的 basic solutions 对应的 linearly independent constraints 有 \(n-1\) 个是相同的时, 我们就称它们是 adjacent. adjacent bases 的定义也是类似的.

The full row rank assumption on \(\mathbf{A}\)

Theorem

Let \(P=\{\mathbf{x} | \mathbf{Ax} = \mathbf{b}, \mathbf{x} \geq \mathbf{0}\}\) be a nonempty polyhedron, where \(\mathbf{A}\) is a matrix of dimensions \(m \times n\), with rows \(\mathbf{a}_{1}', \dots, \mathbf{a}_{m}'\).

Suppose that \(\mathrm{rank}(A) = k < m\) and that the rows \(\mathbf{a}_{i_{1}}', \dots, \mathbf{a}_{i_{k}}'\) are linearly independent. Consider the polydron

\[Q = \{\mathbf{x} | \mathbf{a}_{i_{1}}'\mathbf{x} = b_{i}, \dots, \mathbf{a}_{i_{k}}'\mathbf{x} = b_{i_{k}}, \mathbf{x} \geq \mathbf{0}\}.\]

Then \(Q=P\).

根据此定理, 我们可以得知, 只要满足 feasible set 是非空的, 任意 standard form 的 LP prob 都可以 reduce 到一个等价的且所有 equality constraints 都是 linearly independent 的 LP prob.

Degeneracy

在 general form 下约束形式是 \(\geq\), 那么自然 active constraints 的数量是可以大于 \(n\) 的, 此时我们就称我们有一个 degenerate basic solution.

Degenerate basic solution

A basic solution \(\mathbf{x} \in \mathfrak{R}^n\) is said to be degenerate if more than \(n\) of the constraints are active at \(\mathbf{x}\).

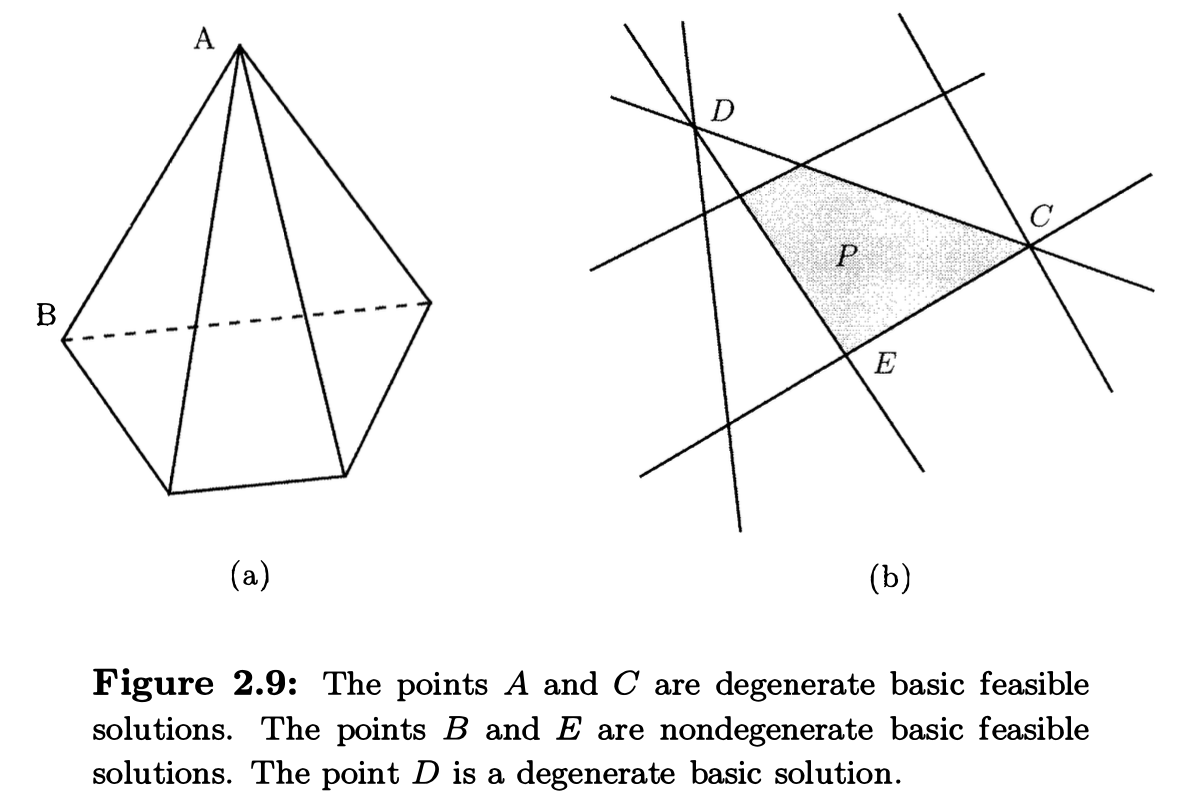
Degeneracy in standard form polyhedra

Definition

Consider the standard form polyhedron \(P = \{\mathbf{x} \in \mathfrak{R}^n | \mathbf{Ax} = \mathbf{b}, \mathbf{x} \geq \mathbf{0}\}\) and let \(\mathbf{x}\) be a basic solution. Let \(m\) be the number of rows of \(\mathbf{A}\). The vector \(\mathbf{x}\) is a degenerate basic solution if more than \(n - m\) of the components of \(\mathbf{x}\) are zero.

这算是上一个定义的 special case.

Note

注意区分它与 row rank \(< m\) 的情况. 这里的产生原因不是 row rank 而是 \(\mathbf{A, b}\) 较为特殊.

常见的题目中, \(\mathbf{A}\) 和 \(\mathbf{b}\) 通常具有一个特殊的结构来达到 degeneracy. 不过 degeneracy 往往比这个 argument 看上去更常见.

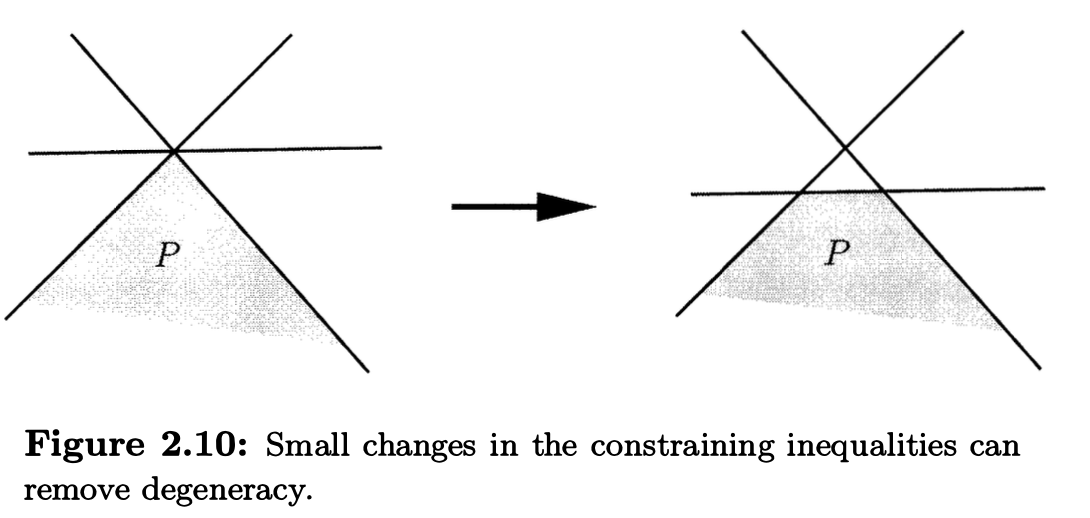
在 standard form polyhedra 中对 degeneracy 进行 visualize, 我们不妨令 \(n-m=2\) 并考虑 feasible set 在这个 2D 下的投影. 通过下图的例子, 我们可以看出要构造出 degeneracy, 我们首先要找到 \(B\) 点这样的特殊点, 然后从它的几个交线中任意选出 2 条作为 nonbasic variables 满足的条件, 其余的 variables 则设为 basic variables, 这样的选择往往有多个.

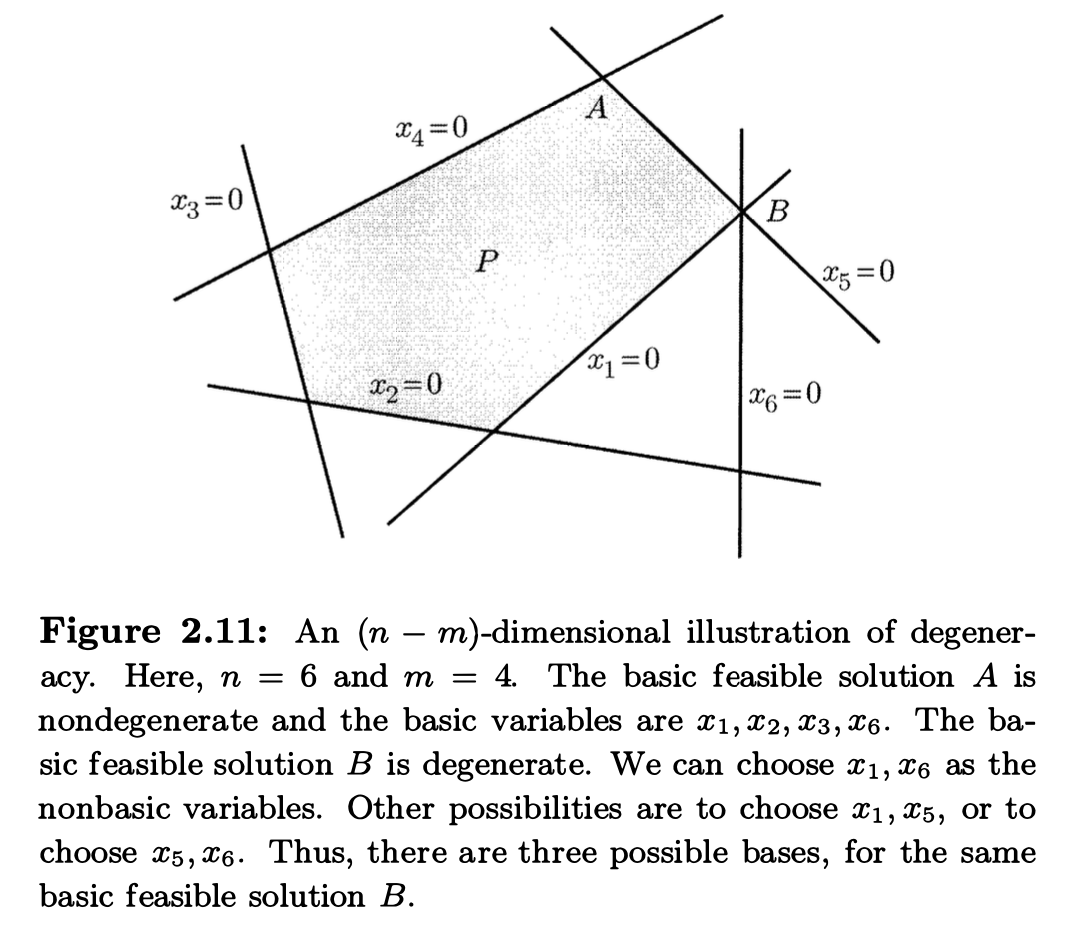
Degeneracy is not a purely geometric property

basic feasible solution 的 degeneracy 并不是一个 geometric property, 而是取决于一个 polyhedron 特定的 representation.

在某个 representation 下是 degenerate 的 basic feasible solution 在另一个 representation 可以是 nondegenerate 的. 如果一个 basic feasible solution 在某个特定的 standard form representation 下是 degenerate 的, 那么可以证明它在同一 polyhedron 的任何 standard form representation 下都是 degenerate 的.

Existence of extreme points

这一小节我们讨论 polyhedron 具有至少一个 extreme point 的充要条件.

下图启发我们 extreme point 的存在取决于这个 polyhedron 是否包含一个 infinite line.

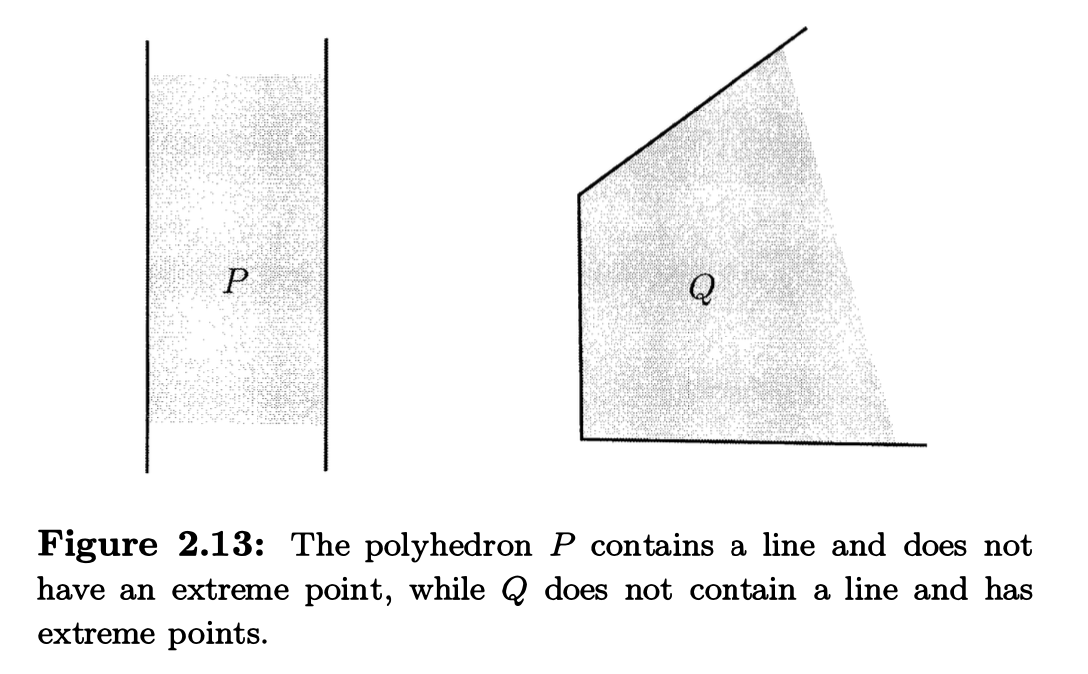
Definition

A polyhedron \(P \subset \mathfrak{R}^n\) contains a line if there exists a vector \(\mathbf{x} \in P\) and a nonzero vector \(\mathbf{d} \in \mathfrak{R}^n\) such that \(\mathbf{x} + \lambda \mathbf{d} \in P\) for all scalars \(\lambda\).

Theorem

Suppose that the polyhedron \(P = \{\mathbf{x} \in \mathfrak{R}^n | \mathbf{a}_{i}' \mathbf{x} \geq b_{i}, i = 1, \dots, m\}\) is nonempty. Then, the following are equivalent:

1. The polyhedron \(P\) has at least one extreme point.
2. The polyhedron \(P\) does not contain a line.
3. There exist \(n\) vectors out of the family \(\mathbf{a}_{1}, \dots, \mathbf{a}_{m}\), which are linearly independent.

Proof

1 \(\implies\) 3:

extreme point 等价于 basic feasible solution, 因此必然存在 \(n\) 个线性无关的约束向量.

2 \(\implies\) 1:

我们首先证明若 \(P\) 不包含 line, 则它有 basic feasible solution, 因而有 extreme point.

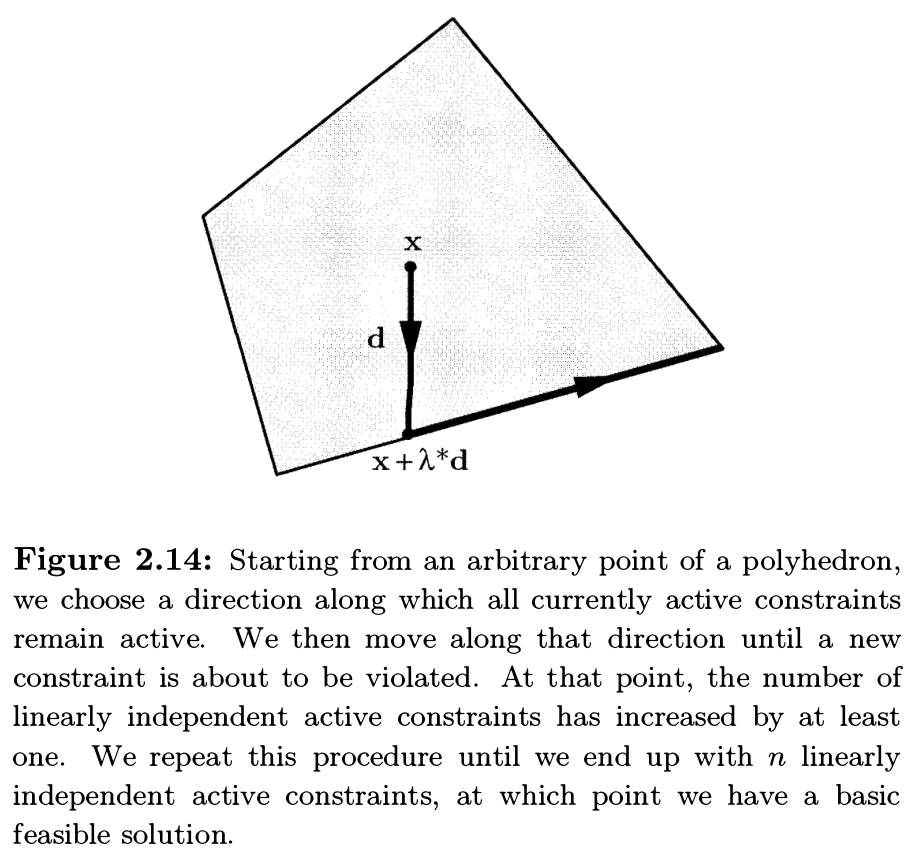
上方的图示是此条证明的 intuition, 据此很容易想到具体的证明过程, 因此不再赘述.

3 \(\implies\) 2:

反证法, 假设 \(P\) 包含一条 line, 即存在 \(\mathbf{x} \in P, \mathbf{d} \in \mathfrak{R}^n, s.t. \forall\lambda \in \mathfrak{R}, \mathbf{x}+\lambda \mathbf{d} \in P\).

设 \(n\) 个线性无关的约束向量的下标集合为 \(I\), 则 \(\exists i \in I, s.t. \mathbf{a}_{i}'\mathbf{d} \neq 0\). 不失一般性地, 我们令 \(\mathbf{a}_{i}'\mathbf{d} < 0\). 则当 \(\lambda\) 足够大时, 必然有 \(\mathbf{a}_{i}'(\mathbf{x}+\lambda \mathbf{d}) < b_{i}\), 即 \(\mathbf{x}+\lambda \mathbf{d} \notin P\), 与假设矛盾, 因此 \(P\) 不包含 line.

Note

一个 bounded polyhedron 必不包含一条 line, 类似地, positive orthant \(\{\mathbf{x} | \mathbf{x} \geq \mathbf{0}\}\) 也不包含一条 line, 由于 standard form 的 polyhedron 包含了 positive orthant, 因此它也不会包含一条 line.

Corollary

Every nonempty bounded polyhedron and every nonempty polyhedron in standard form has at least one basic feasible solution.

Optimality of extreme points

Theorem

Consider the linear programming problem of minimizing \(\mathbf{c'x}\) over a polyhedron \(P\). Suppose that \(P\) has at least one extreme point and that there exists an optimal solution. Then, there exists an optimal solution which is an extreme point of \(P\).

Proof

令 \(Q\) 为 optimal solutions 的集合, 我们假设它是非空的. 令 \(P=\{\mathbf{x} \in \mathfrak{R}^n | \mathbf{Ax} \geq \mathbf{b}\}\) 为 general form 的约束条件的 polyhedron, 不妨设 \(\mathbf{c'x}\) 的 optimal value 为 \(v\), 于是 \(Q = \{\mathbf{x} \in \mathfrak{R}^n | \mathbf{Ax} \geq \mathbf{b}, \mathbf{c'x} = v\}\) 也是一个 polyhedron, 并且 \(Q \subset P\), 因为 \(P\) 不存在 line (\(\leftarrow\) 存在 extreme point), 因此 \(Q\) 也不存在 line, 从而 \(Q\) 也存在 extreme point.

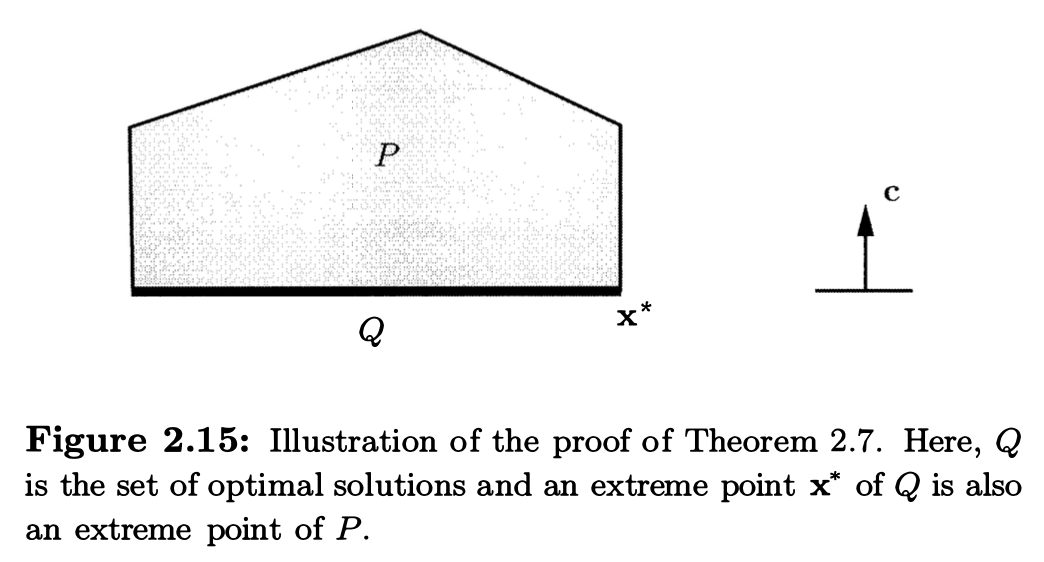
设 \(\mathbf{x}^*\) 是 \(Q\) 的一个 extreme point, 我们证明它同时也是 \(P\) 的一个 extreme point. 我们不妨利用反证法, 从它的逆否命题入手, 即若 \(x^*\) 不是 \(P\) 的 extreme point, 那么它也不会是 \(Q\) 的 extreme point, 然后导出矛盾.

假设 \(\mathbf{x}^*\) 不是 \(P\) 的 extreme point, 那么存在 \(\mathbf{y,z} \in P, \lambda \in [0, 1], \text{s.t. } \mathbf{x}=\lambda\mathbf{y}+(1-\lambda)\mathbf{z}\). 由于 \(\mathbf{x} \in Q\), 因此 \(\mathbf{c'x}=\mathbf{c'}(\lambda \mathbf{y}+(1-\lambda)\mathbf{z})=v\). 因为 \(v\) 是 optimal value, 所以 \(\mathbf{c'y} \geq v, \mathbf{c'z} \geq v\). 要满足上面的等式当且仅当 \(\mathbf{c'y}=\mathbf{c'y}=v\), 即 \(\mathbf{y,z} \in Q\), 这与 \(\mathbf{x}\) 是 \(Q\) 中的 extreme point 矛盾. 因此 \(Q\) 中的 extreme point 一定也是 \(P\) 中的 extreme point.

又 \(Q\) 是 optimal solution 的集合, 因此 \(Q\) 中的 extreme points 一定属于 optimal solutions, 从而 \(P\) 的 extreme points 中必然存在 optimal solution.

上述定理可以 extend to 不包含 line 的 polyhedra in standard form 和 bounded polyhedra.

下面的定理更强, 它不假定 optimal solution 的存在然后证明了当 optimal cost 是 finite 时一定会存在 optimal solution.

Theorem

Consider the linear programming problem of minimizing \(\mathbf{c'x}\) over a polyhedron \(P\). Suppose that \(P\) has at least one extreme point. Then, either the optimal cost is equal to \(-\infty\), or there exists an extreme point which is optimal.

Proof

此定理的证明本质和上一定理的证明一样, 不同之处在于这里我们证明当我们朝某个 basic feasible solution 移动的过程, cost 也是非递增的. 我们会使用到下列术语: 若 \(P\) 中的元素 \(\mathbf{x}\) 能找到的满足 active at \(\mathbf{x}\) 同时是 linearly independent 的约束数量最大值为 \(k\), 我们就称 \(\mathbf{x}\) 的 \(\mathrm{rank}\) 为 \(k\).

从下图可以看出这个证明的 intuition.

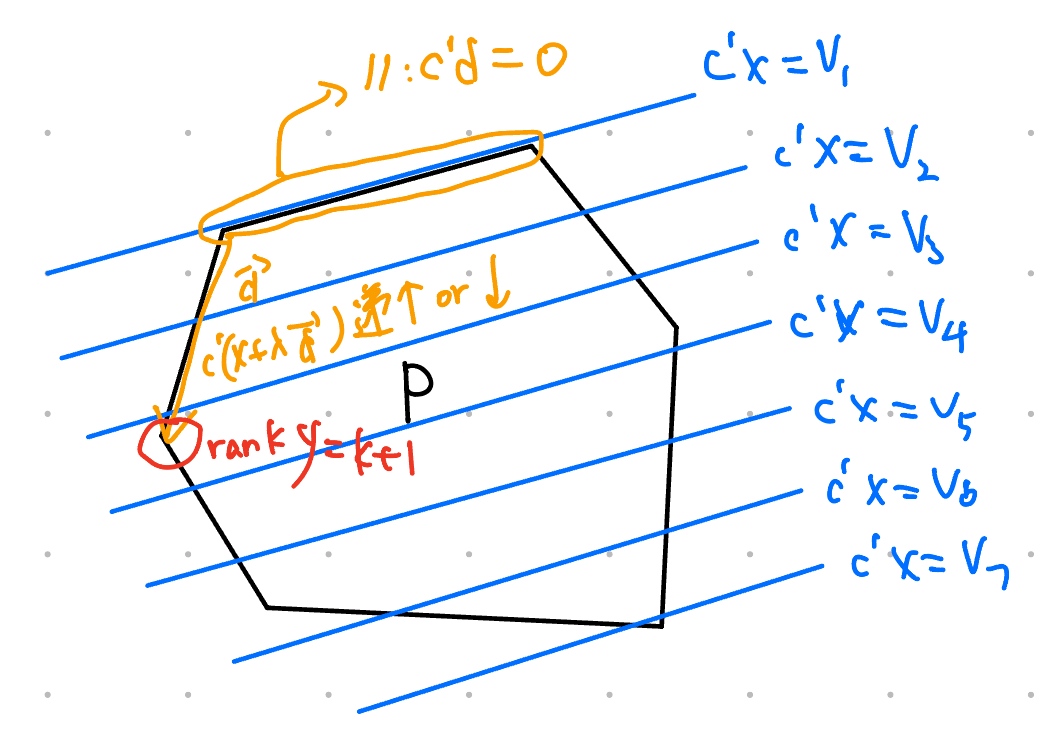
首先我们假设 optimal cost 是 finite 的. 令 \(P = \{\mathbf{x} \in \mathfrak{R}^n | \mathbf{Ax} \geq \mathbf{b}\}\), 考虑其中 \(\mathrm{rank}(x) = k < n\) 的元素 \(\mathbf{x}\). 之后我们将证明我们总能找到 \(\mathbf{y}\) 满足 \(\mathrm{rank}(y)>\mathrm{rank}(x)\) 且 \(\mathbf{c'y} \leq \mathbf{c'x}\). 不妨设 \(I=\{i | \mathbf{a}_{i}'\mathbf{x} = b_{i}\}\), 则 \(\lvert I \rvert=k<n\), 因此我们总能找到 \(\mathbf{d} \in \mathfrak{R}^n, \text{s.t. } \mathbf{a}_{i}'\mathbf{d}=0, \forall i \in I\), 并且我们可以保证可以找到同时满足 \(\mathbf{c'd} \leq 0\) 的 \(\mathbf{d}\).

先考虑 \(\mathbf{c'd} < 0\) 的情况. 设 \(\mathbf{y}=\mathbf{x}+\lambda \mathbf{d}\), 为了使 \(\mathrm{cost}(\mathbf{y}) < \mathrm{cost}(\mathbf{x})\) 我们令 \(\lambda > 0\), 此时所有的 \(\mathbf{y}\) 构成一条 half-line. 沿着这条 half-line 走 (\(\lambda\) 增大), 由于 \(P\) 不包含一条 line (\(\leftarrow\) 存在 extreme point), 因此我们必然会到达一个点, 它满足 \(\lambda^* > 0, \mathbf{a}'_{i}(\mathbf{x}+\lambda^{*}\mathbf{d})=b_{i}, \forall i \in I\) 并且会有 \(\exists j \not\in I, \text{s.t. } \mathbf{a}'_{j}(\mathbf{x} + \lambda^{*}\mathbf{d})=b_{j}\). 我们令 \(\mathbf{y}^*=\mathbf{x} + \lambda^{*}\mathbf{d}\), 注意到 \(\mathbf{c'y} < \mathbf{c'x}\) 且 \(\mathbf{a_{j}}\) 必然与 \(\mathbf{a}_{i}, \forall i \in I\) 满足 linearly independent, 于是 \(\mathrm{rank}(\mathbf{y}^*) \geq k+1\).

然后考虑 \(\mathbf{c'd}=0\). 此时 \(\lambda\) 可以取任意实数, 都会满足 \(\mathrm{cost}(\mathbf{y}) = \mathrm{cost}(\mathbf{x})\), 并且对应的路径是一条 line, 与上一情况相同, 无论我们往哪头走都一定能找到一个 \(\mathbf{y}^*\) 使得 \(\mathrm{rank}(\mathbf{y}^*) \geq k+1, \mathrm{cost}(\mathbf{y}^*)=\mathrm{cost}(\mathbf{x})\).

无论哪种情况, 我们都能找到一个 rank 更大同时 cost 不小于 \(\mathbf{x}\) 的点, 不断重复上述过程, 我们总能找到一个点 \(\mathbf{w}\) 满足 rank = \(n\) (\(\to \mathbf{w}\) 是一个 basic feasible solution) 并且 \(\mathbf{c'w} \leq \mathbf{c'x}\).

综上所述, 我们设 \(\mathbf{w^1}, \dots, \mathbf{w}^r\) 为 \(P\) 的 basic feasible solutions, 令 \(\mathbf{w}^*\) 为 cost 最小的 solution. 根据上述讨论, 对于任意的 \(\mathbf{x} \in P\), 我们都能找到一个 \(\mathbf{w}^i\) 满足 \(\mathbf{c'w}^i \leq \mathbf{c'x}\), 于是就有 \(\mathbf{c'w}^* \leq \mathbf{c'x}, \forall \mathbf{x} \in P\), 从而 \(\mathbf{w}^*\) 是 optimal solution.

注意对于一个 general LP prob, 如果 feasible set 没有 extreme points, 那么上述定理不能被直接应用. 而如果我们能将其转化为一个等价的 standard form LP prob, 就可以直接应用上述定理了.

Corollary

Consider the linear programming problem of minimizing \(\mathbf{c'x}\) over a nonempty polyhedron. Then, either the optimal cost is equal to \(-\infty\) or there exists an optimal solution.

Note

注意与 nonlinear cost function 的 optimization problems 进行对比. 例如 minimizing \(1 / x\) subject to \(x \geq 1\) 的问题, optimal cost 并不是 \(-\infty\) 而 optimal solution 却不存在.

Representation of bounded polyhedra

Theorem

A nonempty and bounded polyhedron is the convex hull of its extreme points.

Proof

设这个 polyhedron 为 \(P\), 它的 extreme points 的 convex hull 集合为 \(P'\), 根据 Section 1 中定理, \(P'\) 也是一个 polyhedron, 我们可以通过证明 \((P \subseteq P') \land (P' \subseteq P)\) 来证明该定理.

\(P' \subseteq P\):

将 extreme points 的 convex combination 的式子代入 \(P\) 的约束不等式中显然.

\(P \subseteq P'\):

对书上证明思路的猜测

我们任取 \(P\) 中一个点, 如果它是 extreme point, 那么显然它属于 \(P'\), 因此我们后面只对非 extreme points 进行考虑.

不妨从 \(\mathfrak{R}^{3}\) 开始考虑, 我们取 \(P\) 内部非表面上的任意一点 \(\mathbf{z}\), 再任取一个 extreme point \(\mathbf{y}\), 考虑用 \(\mathbf{y}\) 来表示 \(\mathbf{z}\), 如果我们已经知道 \(\mathbf{y}\) 所在的某一表面上的点可以用该表面上的 extreme points 的 convex combination 表示, 那我们取其中一点 \(\mathbf{u}\), 试试用 \(\mathbf{y}, \mathbf{u}\) 来表示 \(\mathbf{z}\). 然后可以发现 \(\mathbf{u}-\mathbf{z}\) 的信息太少无法表达. 这时, 我们不妨直接确定好这个向量, 把 \(\mathbf{z}\) 到 \(\mathbf{y}\) 所在的表面改为沿着 \(\mathbf{z}-\mathbf{y}\) 走到 \(\mathbf{y}\) 对着的那个平面, 由于 \(P\) 不会包含 line, 因此那个平面上一定会对应一个 \(\mathbf{u}^*=\mathbf{z}+\lambda^*(\mathbf{z}-\mathbf{y})\), 然后我们就有 \(\mathbf{z}=\frac{\mathbf{u}^*+\lambda^*\mathbf{y}}{1+\lambda^*}\), 此时 \(\mathbf{u}^*\) 和 \(\mathbf{y}\) 的系数和恰好为 1, 如果 \(\mathbf{u}^*\) 可以被它所在的平面上的 extreme points 的 convex combination, 那么我们就能用这些 extreme points + \(\mathbf{y}\) 的 convex combination 来表示 \(\mathbf{z}\), 从而证明了 \(P\) 的形状为 3 维时是满足定理的, 这依赖于 2 维情况的证明. 类似地, 当 \(P\) 为 \(k\) 维时, 我们可以用 \(k-1\) 维推导 \(k\) 维的情况, 而 \(P\) 至多是 \(n\) 维的, 因此我们可以对 \(P\) 的维数使用 induction 进行证明.

定义 polyhedron \(P \subset \mathfrak{R}^n\) 的 dimension 为能将 \(P\) 包含在某个 \(k\)-dimensional affine subspace of \(\mathfrak{R}^n\) 的最小的 \(k\). 显然有 \(k \leq n\), 当 \(k=1\) 时, \(P\) 为一个点, 且这个点是它的 extreme point, 定理成立.

假设小于等于 \(k-1\) 维时定理成立, 考虑 \(k(2\leq k \leq n)\) 维的情况.

令 \(P=\{\mathbf{x} \in \mathfrak{R}^n | \mathbf{a}_{i}'\mathbf{x} \leq b_{i}, i=1, \dots, m\}\) 为 \(k\) 维的 polyhedron, 则 \(P\) 包含于一个 \(k\) 维 affine subspace \(S \subset \mathfrak{R}^n\), 它可以被表示为

\[S = \{\mathbf{x}^0+\lambda_{1}\mathbf{x}^1+\cdots+\lambda_{k}\mathbf{x}^k | \lambda_{1}, \dots, \lambda_{k} \in \mathfrak{R}\},\]

其中 \(\mathbf{x}^1, \mathbf{x}^2, \dots, \mathbf{x}^k\) 为 \(\mathfrak{R}^n\) 中线性无关的一组向量. 令 \(\mathbf{f}_{1}, \dots, \mathbf{f}_{n-k} \in \mathfrak{R}^n\) 为 \(n-k\) 个线性无关的向量, 且分别与 \(\mathbf{x}^1, \mathbf{x}^2, \dots, \mathbf{x}^k\) 正交. 设 \(g_{i}=\mathbf{f}_{i}'\mathbf{x}^0, i=1, \dots, n-k\), 则 \(S\) 中的每个元素 \(\mathbf{x}\) 都有 \(\mathbf{f}_{i}'\mathbf{x}=g_{i}, i=1, \dots, n-k\).

任取 \(P\) 中一个非 extreme point \(\mathbf{z}\) 和 extreme point \(\mathbf{y}\), 令 \(\mathbf{u}=\mathbf{z}+\lambda(\mathbf{z}-\mathbf{y}), \lambda>0\), 由于 \(P\) 不包含 line, 因此存在 \(\lambda^* \geq 0\), 使得对于某些 \(i^*\), 有 \(\mathbf{a}_{i^*}'\mathbf{u}^* = b_{i^*}\), 其中 \(\mathbf{u}^*=\mathbf{z}+\lambda^*(\mathbf{z}-\mathbf{y})\), 当 \(\lambda > \lambda^*\) 时有 \(\mathbf{a}_{i^*}'\mathbf{u} < b_{i^*}\), 这说明 \(\mathbf{a}_{i^*}'(\mathbf{z}-\mathbf{y})<0\) . 令 polyhedron

\[Q=\{\mathbf{x} \in \mathfrak{R}^n | \mathbf{a}_{i}'\mathbf{x}\leq b_{i}, i=1, \dots, m, \mathbf{a}_{i^*}'\mathbf{x}=b_{i^*}\} \subset P\]

显然有 \(\mathbf{u}^* \in Q\). 然后我们证明 \(\dim Q \leq k-1\). 因为 \(\mathbf{z}, \mathbf{y} \in S\), 所以 \(\mathbf{f}_{i}'\mathbf{z}=\mathbf{f}_{i}'\mathbf{y}=g_{i}, i=1, \dots, n-k\), 则 \(\mathbf{f}_{i}'(\mathbf{z}-\mathbf{y})=0, \forall i=1, \dots, m\), 这说明 \(\mathbf{z}-\mathbf{y}\) 与 \(\mathbf{f}_{1}, \dots, \mathbf{f}_{n-k}\) 正交, 若 \(\mathbf{a}_{i^*}\) 可以用 \(\mathbf{f}_{1}, \dots, \mathbf{f}_{n-k}\) 的线性组合表示, 则 \(\mathbf{a}_{i^*}'(\mathbf{z}-\mathbf{y})=0\), 与事实矛盾, 因此 \(\mathbf{a}_{i^*}\) 与 \(\mathbf{f}_{1}, \dots, \mathbf{f}_{n-k}\) 线性无关. 对于解空间为 \(S\) 的线性方程组 \(\mathbf{f}_{i}'\mathbf{x}=g_{i}, \forall i=1, \dots, n-k, \mathbf{x} \in \mathfrak{R}^n\), 我们加上方程 \(\mathbf{a}_{i^*}'\mathbf{x}=b_{i^*}\), 由于 \(\mathbf{f}_{1}, \dots, \mathbf{f}_{n-k}, \mathbf{a}_{i^*}\) 线性无关, 因此它的解空间为 \(n-(n-k+1)=k-1\)-dimensional affine subspace of \(\mathfrak{R}^n\), 设其为 \(S'\), 显然 \(S' \subset S\), 并且 \(Q \subseteq S'\), 因此 \(\dim Q \leq k-1\), 根据假设, \(Q\) 上的所有点可以用它的 extreme points 的 convex combination 表示, 因此 \(\mathbf{u}^*\) 可以被表示为

\[\mathbf{u}^* = \sum_{i \in I} \lambda_{i}\mathbf{v}_{i}\]

其中 \(\sum_{i \in I}\lambda_{i}=1\), \(I\) 为 \(Q\) 的 extreme points \(\mathbf{v}_{i}\) 的下标集合. 根据前面的定理可知, \(Q \subseteq P\) 的 extreme points 也会是 \(P\) 的 extreme points, 从而 \(\mathbf{u}^*\) 可以被 \(P\) 的 extreme points \(\mathbf{v}_{i}, i \in I\) 的 convex combination 表示. 我们又有 \(\mathbf{z}=\frac{\mathbf{u}^* + \lambda^* \mathbf{y}}{1+\lambda^*}\), 因此

\[\mathbf{z} = \frac{\lambda^*}{1+\lambda^*}\mathbf{y} + \sum_{i \in I} \frac{\lambda_{i}}{1+\lambda^*}\mathbf{v}_{i}\]

其中 \(\mathbf{y}, \mathbf{v}_{i}, i \in I\) 为 \(P\) 的 extreme points, 且 \(\frac{\lambda^*}{1+\lambda^*}+\frac{\sum_{i \in I}\lambda_{i}}{1+\lambda^*}=1\), 因此 \(\mathbf{z}\) 可以用 \(P\) 的 extreme points 的 convex combination 表示, 这说明 \(P \subseteq P'\).

Projections of polyhedra: Fourier-Motzkin elimination

Fourier-Motzkin elimination 是解决 LP prob 的最老的办法, 由于它步骤繁多, 因此并不实用, 但是它给我们带来了许多有趣的 corollaries.

这个方法的关键点在于 projection: 如果 \(\mathbf{x}=(x_{1}, \dots, x_{n})\) 是 \(\mathfrak{R}^n\) 中的一个 vector 并且 \(k \leq n\), 则 projection mapping \(\pi_{k}: \mathfrak{R}^{n} \to \mathfrak{R}^{k}\) 将 \(\mathbf{x}\) 映射为它的前 \(k\) 个 coordinates:

\[\pi_{k}(\mathbf{x}) = \pi_{k}(x_{1}, \dots, x_{n}) = (x_{1}, \dots, x_{n}).\]

我们还对集合 \(S \subset \mathfrak{R}^n\) 定义 projection

\[\begin{align} \Pi_{k}(S) &= \{\pi_{k}(\mathbf{x})|\mathbf{x} \in S\} \\ &= \{(x_{1}, \dots, x_{k}) | \text{there exist } x_{k+1}, \dots, x_{n} \text{ s.t. } (x_{1}, \dots, x_{n}) \in S\} \end{align}\]

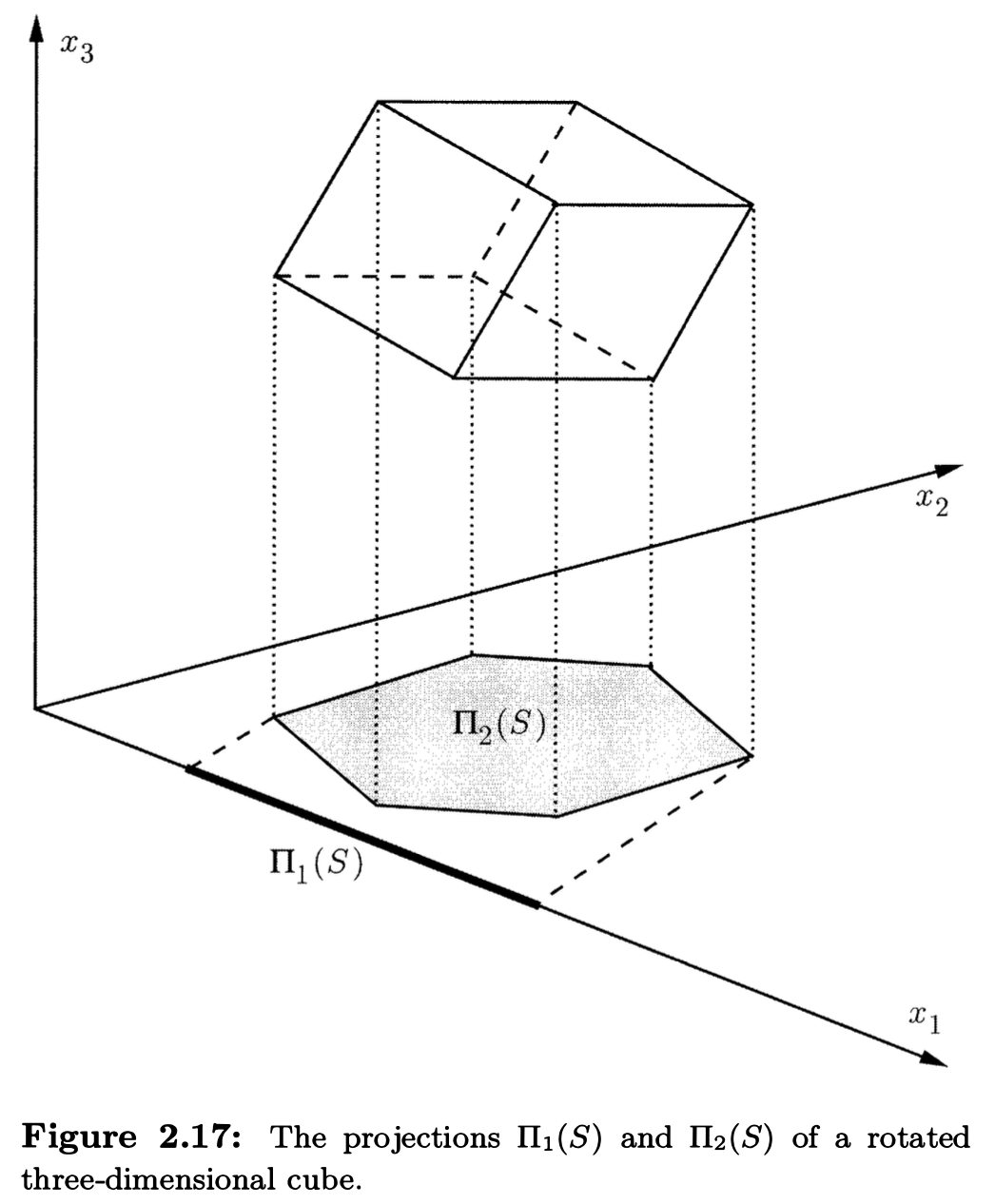
不难发现, \(P \subset \mathfrak{R}^n\) 非空 \(\leftrightarrow\) \(\Pi_{n-1}(P) \subset \mathfrak{R}^{n-1}\) 非空, 从而我们根据 \(\Pi_{1}(P)\) 是否非空即可判断 polyhedron \(P\) 是否非空.

现在我们考虑 elimination method 是如何构造 projection \(\Pi_{n-1}(P)\) 来消除 \(x_{n}\) 的.

Elimination algorithm

1. Rewrite each constraint \(\sum_{j=1}^{n} a_{ij}x_{j} \geq b_{i}\) in the form \(\(a_{in}x_{n} \geq -\sum_{j=1}^{n-1}a_{ij}x_{j}+b_{i}, \quad i=1, \dots, m;\)\) if \(a_{in}\not=0\), divide both sides by \(a_{in}\). By letting \(\mathbf{\bar{x}}=(x_{1, \dots, x_{n-1}})\), we obtain an equivalent representation of \(P\) involving the following constraints:

\(\begin{aligned} x_{n} & \geq d_{i}+\mathbf{f}_{i}^{\prime} \overline{\mathbf{x}}, & & \text { if } a_{i n}>0, \\ d_{j}+\mathbf{f}_{j}^{\prime} \overline{\mathbf{x}} & \geq x_{n}, & & \text { if } a_{j n}<0, \\ 0 & \geq d_{k}+\mathbf{f}_{k}^{\prime} \overline{\mathbf{x}}, & & \text { if } a_{k n}=0. \end{aligned}\)

Here, each \(d_{i}, d_{j}, d_{k}\) is a scalar, and each \(\mathbf{f}_{i}, \mathbf{f}_{j}, \mathbf{f}_{k}\) is a vector in \(\mathfrak{R}^{n-1}\).

2. Let \(Q\) be the polyhedron in \(\mathfrak{R}^{n-1}\) defined by the constraints

\(\begin{aligned} d_{j}+\mathbf{f}_{j}^{\prime} \overline{\mathbf{x}} & \geq d_{i}+\mathbf{f}_{i}^{\prime} \overline{\mathbf{x}}, & & \text { if } a_{i n}>0 \text { and } a_{j n}<0, \\ 0 & \geq d_{k}+\mathbf{f}_{k}^{\prime} \overline{\mathbf{x}}, & & \text { if } a_{k n}=0. \end{aligned}\)

Theorem

The polyhedron \(Q\) constructed by the elimination al­gorithm is equal to the projection \(\Pi_{n-1}(P)\) of \(P\).

可以看出, 只要我们允许 elimination algorithm \(n-1\) 次就能得到 \(\Pi_{1}(P)\). 不幸的是, 每跑一次约束条件的数量就会剧烈增长. 尽管最终得到 \(\Pi_{1}(P)\) 是一维的, 几乎所有 constraints 都是多余的, 但是我们仍然需要对 constraints 进行 enumerate 才能决定它是否是 redundant 的.

根据算法的步骤结合上述定理, 对于 polyhedron \(P\), 任意 \(1 \leq k \leq n\) 的 projection \(\Pi_{k}(P)\) 仍然是一个 polyhedron.

Corollary

Let \(P \subset \mathfrak{R}^{n+k}\) be a polyhedron. Then the set

\[\{\mathbf{x} \in \mathfrak{R}^{n} | \text{there exists } \mathbf{y} \in \mathfrak{R}^{k} \text{ such that } (\mathbf{x}, \mathbf{y}) \in P\}\]

is also a polyhedron.

Corollary

Let \(P \subset \mathfrak{R}^n\) be a polyhedron and let \(\mathbf{A}\) be an \(m \times n\) matrix. Then, the set \(Q=\{\mathbf{Ax} | \mathbf{x} \in P\}\) is also a polyhedron.

Proof

利用上一条 corollary 证明.

很容易构造出 \(R = \{(\mathbf{x}, \mathbf{y}) \in \mathfrak{R}^{n+m} | \mathbf{Ax}=\mathbf{y}, \mathbf{x} \in P\}\), \(\mathbf{Ax}=\mathbf{y}\) 显然是 standard form polyhedron 的约束, 加上 \(\mathbf{x} \in P\) 相当于在 \(P\) 的约束基础上增加一些约束, 因此 \(R\) 也会是一个 polyhedron. 而 \(Q=\{\mathbf{y} \in \mathfrak{R}^m | \text{there exists }x \in \mathfrak{R}^n \text{ such that }\mathbf{Ax}=\mathbf{y}, \mathbf{x} \in P\}\) 则是 \(R\) 在 \(\mathbf{y}\) 轴上的 projection, 因此 \(Q\) 也是 polyhedron.

Corollary

The convex hull of a finite number of vectors is a polyhedron.

Proof

把 convex hull

\[\left\{\sum_{i=1}^{k}\lambda_{i}\mathbf{x}^{i} \vert \sum_{i=1}^{k}\lambda_{i}=1, \lambda_{i} \geq 0 \right\}\]

看作将 polyhedron

\[\left\{(\lambda_{1}, \dots, \lambda_{k}) | \sum_{i=1}^{k}\lambda_{i}=1, \lambda_{i} \geq 0 \right\}\]

左乘上矩阵 \(\mathbf{X}\) 的线性映射, 然后根据前一个引理即可得证.

最后我们考虑 elimination algorithm 如何应用于 LP prob 中. 假设我们的目标是 minimize \(\mathbf{c'x}\) subject to a polyhedron \(P\). 我们定义一个新的 variable \(x_{0}=\mathbf{c'x}\), 然后我们运行 \(n\) 次 elimination algorithm 来消除 \(x_{1}, \dots, x_{n}\), 就会剩下集合

\[ Q = \{x_{0} | \text{there exists } \mathbf{x} \in P \text{ such that } x_{0}=\mathbf{c'x}\}, \]

此时 optimal cost 就是 \(Q\) 中最小的元素, 而 optimal solution \(\mathbf{x}\) 可以通过 backtracking 找到.

red pink purple deep purple indigo blue light blue cyan teal green light green lime yellow amber orange deep orange brown grey blue grey black white

Comments