DPV Chapter 2: Divide-and-conquer algorithms

divide-and-conquer 通过以下步骤来解决一个问题:

1. 将问题拆分称同类型的 subproblems
2. 递归解决 subproblems
3. 正确合并 subproblems 的 answers

Multiplication

假设 \(x, y\) 是 \(n\)-bit number, 其中 \(n\) 是 2 的幂.

将 \(x, y\) 按照 bit 拆成左右两个等长的部分, 则

\[xy = 2^{n} x_{L} y_{L} + 2^{n / 2} (x_{L}y_{R} + x_{R}y_{L}) + x_{R} y_{R}\]

可以发现, \(x_{L}y_{R} + x_{R}y_{L} = (x_{L} + x_{R})(y_{L} + y_{R}) - x_{L}y_{L} - x_{R}y_{R}\), 代入上式之后我们就将 4 次 \(n / 2\)-bit 乘法转为了 3 次, 总耗时的 recurrence relation 为

\[ T(n) = 3T(n / 2) + O(n) \]

此时, 时间复杂度约为 \(O(n^{1.59})\).

Recurrence relations

divide-and-conquer 算法一般遵循一个 generic pattern: 解决一个大小为 \(n\) 的问题, 将其拆分为 \(a\) 个大小 \(n / b\) 的 subproblems, 将这些 subproblems 合并需要 \(O(n^d)\), 其中 \(a, b, d > 0\). 最终我们可以用方程 \(T(n) = aT(\lceil n / b \rceil) + O(n^d)\) 来表示它的耗时.

Master theorem

If \(T(n) = aT(\lceil n / b \rceil) + O(n^d)\) for some constants \(a>0, b > 1\), and \(d \ge 0\), then

\[T(n) = \begin{cases} O(n^d) &\text{if } d > \log_{b}a \\ O(n^d \log n) &\text{if } d = \log_{b}a \\ O(n^{\log_{b}a}) &\text{if } d < \log_{b}a. \end{cases}\]

Mergesort

running time 为:

\[T(n) = 2T(n / 2) + O(n)\]

或者 \(O(n \log n)\).

Median

考虑 general version: 求解第 \(k\) 大的数.

由于我们不关心其它数之间的相对大小关系, 因此考虑采用 selection 来解决.

A randomized divide-and-conquer algorithm for selection

从数列中随机选择一个数 \(v\), 然后我们可以将数列分为三个部分, 其中 \(S_{L}\) 为小于 \(v\) 的数, \(S_{v}\) 为等于 \(v\) 的部分, \(S_{R}\) 为大于 \(v\) 的部分. 这样一来, 如果 \(k \leq \lvert S_{L} \rvert\) 那么我们在 \(S_{L}\) 中递归寻找第 \(k\) 大的数; 如果 \(\lvert S_{L} \rvert < k \leq \lvert S_{L} \rvert + \lvert S_{v} \rvert\) 那么第 \(k\) 大的数就是 \(v\); 否则在 \(S_{R}\) 中递归寻找第 \(k - |S_{L}|-|S_{v}|\) 大的数. 即:

\[ \operatorname{selection}(S, k) = \begin{cases} \operatorname{selection}(S_{L}, k) &\text{if } k \leq |S_{L}| \\ v &\text{if } |S_{L}| < k \leq |S_{L}| + |S_{v}| \\ \operatorname{selection}(S_{R}, k - |S_{L}| - |S_{v}|) &\text{if } k > |S_{L}| + |S_{v}|. \end{cases} \]

Efficiency analysis

先考虑 worst-case: \(v\) 恰好是数列中的最大值, 那么上述算法求解 median 的时间复杂度约为

\[n + (n - 1) + \cdots + \frac{n}{2} = \Theta(n^2)\]

如果是 best-case, 那么显然耗时 \(T(n) = n\).

考虑 average-case. 上述算法最大的好处是每进行一次, 就能将 \(n\) 的规模缩小到至多 \(\max\{\lvert S_{L} \rvert, |S_{R}|\}\), 显然当 \(v\) 选的越靠近 median 就缩小的越多, 具体一点, 当 \(v\) 的排名在 \(\frac{1}{4}n \sim \frac{3}{4}n\) 时我们就认为这个 \(v\) 是好的 (good). 从概率上来说, 我们随机到一个 good \(v\) 的概率是 \(\frac{1}{2}\).

经过一次分裂, 新数列的期望大小是 \(\frac{3}{4}n\), 设 \(T(n)\) 为大小 \(n\) 的数列的 expected running time, 则有

\[T(n) \leq T(3n / 4) + O(n)\]

两边取 expectation, 可以得到 \(T(n) = O(n)\).

Matrix multiplication

假设 \(X, Y\) 是两个 \(n \times n\) 的矩阵, 那么求解 \(X \times Y\) 中任意一个 entry 需要进行 \(n\) 次乘法运算和 \(n\) 次加法运算, 方便起见, 我们不考虑乘法与加法运算的时间, 那么求解 \(X \times Y\) 的时间复杂度为 \(O(n^3)\).

仍然考虑 divide-and-conquer 算法, 将问题拆分成子问题, 不妨将 \(X, Y\) 分别拆成 4 块, 每一块的大小都是 \(n / 2 \times n / 2\), 如下

\[ X = \begin{bmatrix} A & B \\ C & D \end{bmatrix}, \quad Y = \begin{bmatrix} E & F \\ G & H \end{bmatrix}. \]

于是有

\[ XY = \begin{bmatrix} AE+BG & AF+BH \\ CE+DG & CF+DH \end{bmatrix} \]

我们将其拆分成了 8 个 \(n / 2 \times n / 2\) 的矩阵乘法和几个 \(O(n^2)\) 的矩阵加法, 因此总的 running time 为

\[T(n) = 8T(n / 2) + O(n^2)\]

根据 Master theorem, 此时的时间复杂度仍然是 \(O(n^3)\).

事实上, 上式可以将 8 优化为 7, 这种算法由 Strassen 提出:

\[ XY = \begin{bmatrix} P_{5}+P_{4}-P_{2}+P_{6} & P_{1}+P_{2} \\ P_{3}+P_{4} & P_{1}+P_{5}-P_{3}-P_{7} \end{bmatrix} \]

其中

\[ \begin{array} {}P_{1}=A(F-H) \quad &P_{5}=(A+D)(E+H) \\ P_{2}=(A+B)H \quad &P_{6}=(B-D)(G+H) \\ P_{3}=(C+D)E \quad &P_{7}=(A-C)(E+F) \\ P_{4}=D(G-E) \quad \end{array} \]

Note

一个对 Strassen 的思路的可能的猜测是:

1. 首先将 \(AE, BG \dots\) 等 8 个式子合并成两个包含 4 项的式子得到 \(P_{6}, P_{7}\)
2. 然后构造尽可能少的包含 3 项的式子 (\(P_1 \sim P_{4}\)) 来消掉 4 项式拆解得到的项数, 使其能够得到 \(XY\) 中的某一个 entry
3. 多次尝试发现至少还需要一个 4 项式 (\(P_{5}\)) 来补足
4. 最终得到 7 个仅包含 1 次矩阵乘法的式子

当然, 对现在来说对于这种项数只有 \(7\) 项的代数式子完全可以用计算机枚举出来, 但是目前为止还没有出现过 \(6\) 项的式子很大程度上说明优化到 \(7\) 项已是极限, 事实上这也确实是将矩阵拆成 \(n / 2 \times n / 2\) 能化简到的最少的项数了.

最后的时间复杂度为 \(O(n^{\log_{2} 7}) \approx O(n^{2.81})\).

The fast Fourier transform

假设有多项式 \(A(x) = a_{0}+a_{1}x+\cdots+a_{d}x^{d}, B(x) = b_{0}+b_{1}x+\cdots+b_{d}x^d\), 要求 \(C(x) = A(x) \cdot B(x)=c_{0}+c_{1}x+\cdots+c_{2d}x^{2d}\), 显然有

\[c_{k} = \sum_{i=0}^{k} a_{i}b_{k-i}\]

求出 \(c_{k}\) 需要 \(O(k)\) 步, 那么求出所有的系数需要 \(\Theta(d^2)\) 的时间.

回忆前面 integer multiplication 算法, 可以发现如果 \(x=10\) 那么上述多项式求解就成为了 integer multiplication, 但是再仔细思考就会发现 integer multiplication 中的系数都在 \([0, 9]\) 的范围内, 并且存在进位的情况, 而多项式乘法则不然, 如果依然采用类似 Karatsuba 算法的 divide-and-conquer 方法会发现复杂度依然是 \(O(d^2)\).

An alternative representation of polynomials

Fact

A degree-\(d\) polynomial is uniquely characterized by its values at any \(d+1\) distinct points.

Proof

这个事实可以用一点线性代数的知识证明. 假设我们有 \(d+1\) 个不同的点 \((x_{0}, y_{0}), (x_{1}, y_{1}), \dots, (x_{d}, y_{d})\) 并且它们都在 degree 为 \(d\) 的多项式 \(A(x)\) 上.

将 \(A(x_{k})=a_{0}+a_{1}x_{k}+\cdots+a_{d}x_{k}^d=y_{k}\) 写成线性方程组, 然后用矩阵乘积的形式来表达可以得到

\[ \begin{bmatrix}1 & x_{0} & x_{0}^2 & \cdots & x_{0}^d \\1 & x_{1} & x_{1}^2 & \cdots & x_{1}^d \\ \vdots & \vdots & \vdots & \ddots & \vdots \\1 & x_{d} & x_{d}^2 & \cdots & x_{d}^d\end{bmatrix}\begin{bmatrix}a_{0} \\a_{1} \\ \vdots \\a_{d}\end{bmatrix}=\begin{bmatrix}y_{0} \\y_{1} \\ \vdots \\y_{d}\end{bmatrix} \]

将其简写为 \(M \vec{a}=\vec{y}\), 由于这 \(d+1\) 个点互不相同, 因此 \(M\) 很显然是一个 Vandermonde matrix, 并且有 \(\det M \not= 0\), 从而 \(\vec{a}\) 有唯一解, 从而 \(A(x)\) 是唯一确定的.

借此, 我们只需找出 \(2d+1\) 个不同的 \(x\), 通过 \(A(x_{k})\times B(x_{k}) = C(x_{k})\) 来求解每个点的纵坐标值即可唯一确定 \(C(x)\).

最后算法的框架如下:

上述转换视角最大的好处就是将 Multiplication 部分由 \(O(n^2)\) 转化为了 \(O(n)\), 现在的问题在于朴素地计算 Evaluation 部分依然是 \(O(n^2)\) 的复杂度, 还有最后的 Interpolation 的算法未知.

Evaluation by divide-and-conquer

如果希望优化 Evaluation 的速度, 那么有策略地选取 \(n\) 个点是必不可少的. 一种简单的策略就是选择

\[\pm x_{0}, \pm x_{1}, \dots, \pm x_{n / 2 - 1}\]

这样在计算 \(A(x_{i})\) 和 \(A(-x_{i})\) 时有一半的项是重合的, 将 \(A(x)\) 拆成奇数项和偶数项:

\[A(x) = A_{e}(x^2) + xA_{o}(x^2)\]

那么上述优点可以表示为

\[ \begin{aligned} A(x_{i}) &= A_{e}(x_{i}^2) + x_{i} A_{o}(x_{i}^2) \\ A(-x_{i}) &= A_{e}(x_{i}^2) - x_{i} A_{o}(x_{i}^2). \end{aligned} \]

这启发我们, 要计算 \(A(\pm x_{i})\) 只需要计算出 \(A_{e}(x_{i}^2)\) 和 \(A_{o}(x_{i}^2)\) 即可, 二者的问题结构相同, 显然可以用 divide-and-conquer 算法求解然后 \(O(n)\) 合并, 因此在 Evaluation 部分的时间为

\[T(n) = 2T(n / 2) + O(n)\]

也就是 \(O(n \log n)\).

但是问题又来了, 前面的 plus-minus trick 只在递归树的 top level 有效, 在后面的层级中只有正数因此我们无法重复分解 \(n / 2\) 大小的 subproblem 为 \(n / 4\) 大小的 subsubproblems. 这个时候, 我们可以引入复数来弥补.

简单起见, 我们不妨将 \(x_{i}\) 设成复平面的单位圆上的点: \(1, \omega, \omega^2, \dots, \omega^{n-1}\), 其中 \(\omega = e^{2 \pi i / n}\). 引入复数还有一个很大的好处就是将幂操作转化为了复平面上与实轴夹角取倍数的操作, 因此也就存在周期性.

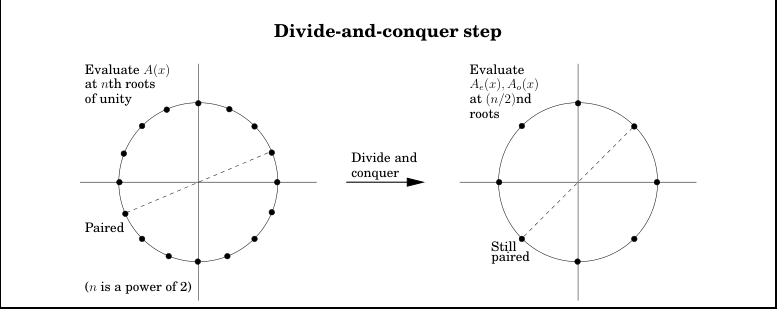
上面提到的算法其实就是 FFT 了:

Interpolation

Interpolation 其实也就是前面 FFT 的逆过程.

根据信号与系统中 Fourier Transform 的知识, FFT 的过程其实就是用 divide-and-conquer 算法加速 DFT (Discrete Fourier Transform) 的过程, 甚至整个 \(A(x)\times B(x)\) 向 \(A(\vec{\omega})\cdot B(\vec{\omega})\) 的转化也和 \((f*g)(t) \xrightarrow{FT} F(\omega) \times G(\omega)\) 不谋而合. 那么不难想到

\[\text{<values>} = \operatorname{FFT}(\text{<coefficients>}, \omega) \implies \text{<coefficients>} = \operatorname{FFT}(\text{<values>}, \omega^{-1})\]

Interpolation resolved

回顾前面的提到过的系数矩阵 \(M\), 当 \(x\) 被 \(n\) 个 \(\omega\) 替代时有

\[ M_{n}(\omega) = \begin{bmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega & \omega^2 & \cdots & \omega^{n-1} \\ 1 & \omega^2 & \omega^4 & \cdots & \omega^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega^{n-1} & \omega^{2(n-1)} & \cdots & \omega^{(n-1)(n-1)} \end{bmatrix} \]

将它的 columns 看成 Fourier basis, 那么 FFT 就是将笛卡尔坐标系中的点 (\(\vec{x}\)) 线性转化为了 Fourier basis, 是一种 rigid rotation. 那么 FFT 的逆操作就是乘上 \(M_{n}(\omega)^{-1}\).

Inversion formula

\[M_{n}(\omega)^{-1} = \frac{1}{n} M_{n}(\omega^{-1}).\]

下面的 lemma 证明了该矩阵的 columns 可以看作一组正交基底.

Lemma

The columns of matrix \(M\) are orthogonal to each other.

A closer look at the fast Fourier transform

The definitive FFT algorithm

FFT 的 input 是 \(n\) 维多项式系数向量 \(\vec{a}\) 和一个复数 \(\omega\). 它将 \(\omega\) 写成 \(M_{n}(\omega)\) 的形式并乘上 \(\vec{a}\) 并返回结果向量. FFT 使用 divide-and-conquer 算法加速矩阵乘法, 如下:

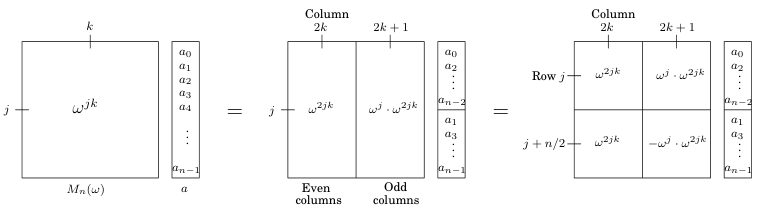
得到的结果向量为如下形式:

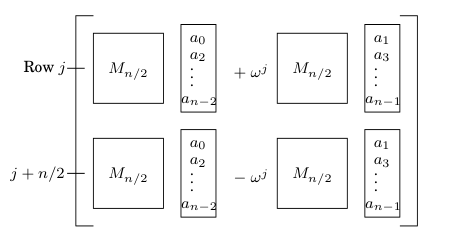
FFT 总的运行时间为 \(T(n) = 2Y(n / 2) + O(n) = O(n \log n)\).

The fast Fourier transform unraveled

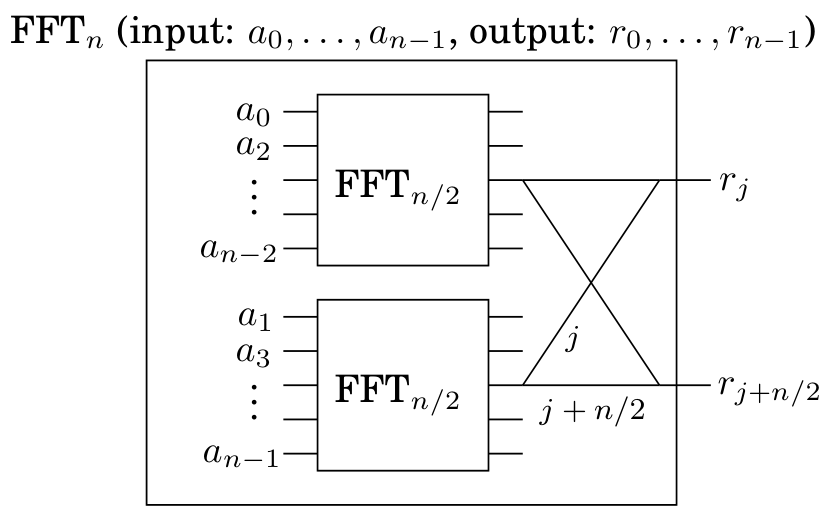
可以看出 \(r_{j}\) 与 \(r_{j + n / 2}\) 的计算式构成一个类似蝴蝶 (butterfly) 的结构.

以 \(n=8\) 为例, 运行 FFT 算法可以得到下图的结构:

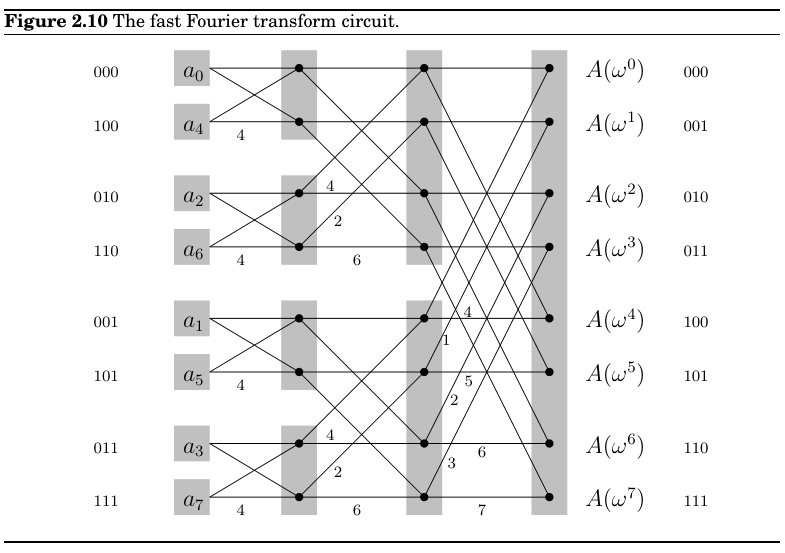
可以发现:

1. \(n\) 个输入会得到 \(\log n\) 个 levels, \(n\) 个 nodes, 以及 \(n \log n\) 次操作.
2. 输入序列会排列成一个 peculiar order, 构成蝶形结构的两个输入之间下标差值刚好为 \(n / 2 = 4\), 而排列后的序列下标的 binary bits 刚好是对应输出顺序的镜像.
3. 从每个 \(a_{j}\) 到每个 \(A(\omega^k)\) 都存在一条 unique path.
4. 在 \(a_{j}\) 到 \(A(\omega^k)\) 的路径上, labels 的和为 \(jk \pmod{8}\), 这表明 \(a_{j}\) 到 \(A(\omega^k)\) 的贡献是 \(a_j \omega^{jk}=a_{j} (\omega^{k})^j\), 符合 Fourier Series.
5. 这种结构很适合 parallel computation, 可以直接在硬件上实现.

代码实现如下:

# AUTHOR: Jelani Nelson
# VERSION: 1.0, 09/13/2022
# BSD 3-Clause

# FFT
import math
import numpy # just for complex conjugate method (numpy.conj(a+ib) is a-ib)

# return smallest power of 2 that is >= n
def hyperceil(n):
  if n == 0:
    return 1
  j = 0
  m = n
  while m > 0:
    j += 1
    m >>= 1
  if 1<<(j-1) == n:
    return n
  else:
    return 1<<j

def fft(a):
  # only works if len(a) is a power of 2
  assert (len(a) == hyperceil(len(a)))
  n = len(a)
  if n == 1:
    return a[:]
  aeven_transform = fft(a[::2]) # even indexed coeffs
  aodd_transform = fft(a[1::2]) # odd indexed coeffs
  w = complex(math.cos(2*math.pi/n), math.sin(2*math.pi/n))
  cur = 1
  ans = []
  for i in range(n):
    ans.append(aeven_transform[i%(n//2)] + cur*aodd_transform[i%(n//2)])
    cur *= w
  return ans

# FAST POLYNOMIAL MULTIPLICATION USING FFT
# a are coeffs of A(x), and b of B(x)
def fast_poly_mult(a, b):
  n = max(len(a), len(b))
  N = hyperceil(2*n-1)
  apad = a + [0]*(N-len(a))
  bpad = b + [0]*(N-len(b))

  ah = fft(apad)
  bh = fft(bpad)
  ch = [a*b for a,b in zip(ah, bh)]

  # can show F^{-1} = (1/N) F~, where ~ is entry-wise complex conjugate
  # then F~ * y = (F * (y~))~ (a fact about complex matrix-vec mult)
  z = fft([numpy.conj(x) for x in ch])
  c = [x.real/N for x in z]

  return c[:len(a)+len(b)-1]

# FAST CROSS-CORRELATION USING FAST POLY MULT
def cross_correlation(x, y):
  assert (len(x) <= len(y))
  return fast_poly_mult(x[::-1], y)[len(x)-1:len(y)]

red pink purple deep purple indigo blue light blue cyan teal green light green lime yellow amber orange deep orange brown grey blue grey black white

Comments