Automata and Language Theory

Key

Finite automata, regular expressions, push-down automata, context-free grammars, pumping lemmas.

Regular Languages

Finite Automata

对于内存容量极小的 computers 来说，finite automata 是一个很好的 model。

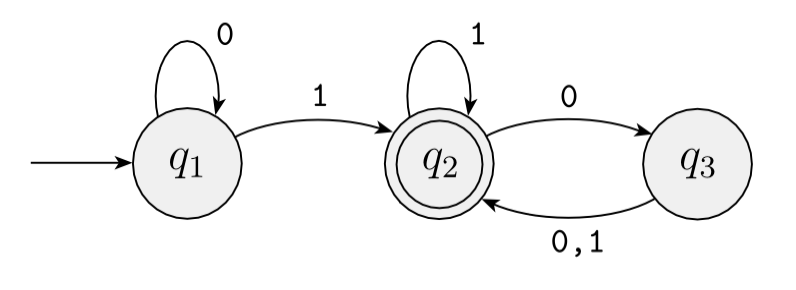
一个 finite automata 由以下 3 个部分组成：

• input: finite string
• out: Accept or Reject
• computation process: 从 start state 开始，读入 input symbols，进行相应的 transition，如果以 accept state 结束则输出 Accept 否则输出 Reject

能让 finite automata \(M_1\) accept 的 strings 的集合记为 \(A\)，我们称 \(A\) 是 \(M_1\) 的语言 (language)，\(M_1\) 可以识别 (recognize) \(A\)，\(A=L(M_1)\) 。

对 finite automata 的 formal definition 如下：

Definition

A finite automaton \(M\) is a 5-tuple \((Q, \Sigma, \delta, q_0, F)\)

1. \(Q\): finite set of states
2. \(\Sigma\): finite set of alphabet symbols
3. \(\delta\): transition functions \(\delta\colon Q\times\Sigma \to Q\)
4. \(q_0\): start state
5. \(F\): set of accept states

对于 string 和 languages 还有以下补充与定义：

Info

• string 是由 \(\Sigma\) 中的 symbols 组成的有限长序列
• language 是 strings 的集合 (finite or infinite)
• empty string \(\varepsilon\) 是长度为 0 的 string
• empty language \(\varnothing\) 是不包含 string 的集合

Definition

\(M\) accepts string \(w=w_1w_2\dots w_n\), each \(w_i\in\sigma\) if there is a sequence of states \(r_0, r_1, r_2, \dots, r_n\in Q\) where:

• \(r_0=q_0\)
• \(r_i=\delta(r_{i-1}, w_i) ,\forall 1\le i\le n\)
• \(r_n\in F\)

Definition

A language is regular if some finite automaton recognizes it.

Example

\(C=\{ w|w \textrm{ has equal numbers of 0s and 1s} \}\) 不是一个 regular language

Proof

把自己想象成一个 finite automata，会发现想要识别 \(C\) 至少需要跟踪 0 和 1 的数量的差值，实际上这个差值是可能无限大的，所需要的 \(Q\) 则是 infinite 的，因此 \(C\) 无法被任何 finite automata 识别，所以 \(C\) 不是一个 regular language

非常不严谨的证明

arithmetic 的研究对象是 numbers，而在 theory of computation 中的研究对象则是 languages。arithmetic 有基本的 operations 来研究 numbers，相应地，我们也可以定义几种 operations 来研究 languages 的 properties。

对于 languages \(A,B\)，我们定义以下三种 operations，称为 regular operations :

Definition

• union: \(A\cup B=\{w|w\in A \, \mathrm{or} \, w\in B\}\)
• concatenation: \(A\circ B=\{ xy|x\in A\, \mathrm{and} \, y\in B \}=AB\)
• star: \(A\ast=\{ x_1\dots x_k|\mathrm{each} \, x_i\in A \, \mathrm{for}\, k\ge 0 \}\)

可以发现对于任意 regular languages，它们的 union 和 concatenation 运算得到的仍然是 regular language.

Theorem

The class of regular languages is closed under the union and concatenation operations.

Proof

（仅 DFA ）
显然采用构造法。

Union:

• \(M_1=(Q_1, \Sigma, \delta_1, q_1, F_1)\) recognizes \(A_1\)
• \(M_2=(Q_2, \Sigma, \delta_2, q_2, F_2)\) recognizes \(A_2\)
• 构造 \(M=(Q, \Sigma, \delta, q_0, F)\) 识别 \(A_1\cup A_2\)
  • \(Q=Q_1\times Q_2\)
  • \(q_0=(q_1, q_2)\)
  • \(\delta((q, r), q)=(\delta_1(q, a), \delta_2(r, a))\)
  • \(F=(F_1\times Q_2)\cup(Q_1\times F_2)\)

Concatenation:

• 使用 DFA 没有一个简单的构造方法。

Nondeterminism

determinism: 给定 machine 的 state，当读入下一个 symbol 时，我们可以确定下一个 state

nondeterminism 是 determinism 的一种 generalization，所以每一个 nondeterministic finite automaton (NFA) 都天生是 deterministic finite automaton (DFA)。

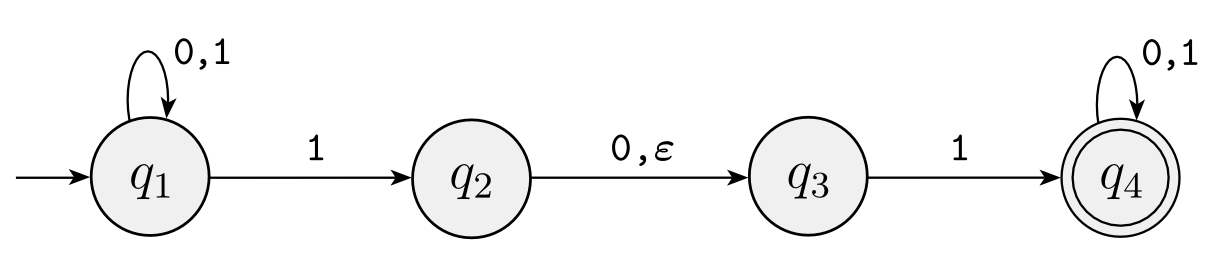
Definition

A nondeterministic finite automaton is a 5-tuple \((Q, \Sigma, \delta, q_0, F)\) where:

1. \(Q\) is a finite set of states,
2. \(\Sigma\) is a finite alphabet,
3. \(\delta\colon Q\times\Sigma_{\epsilon}\to\mathcal{P}(Q)\) is the transition function,
4. \(q_0\in Q\) is the start state, and
5. \(F\cup Q\) is the set of accept states.

对比 DFA，NFA 其实保留了所有可能到达的 states，并且考虑每一个可能性，只要有一个分支被 accept，那么就说明这个 string 是可以被 accept 的，可以分别从三个角度来理解 nondeterminism：

• computational：对于可能到达的 states，每个都 fork 一个新的 parallel thread，任意一个 thread 能够到达 accept state 则 accept
• Mathematical：看成 tree with branches，每一条从根结点 (start state) 到叶子结点 (accept state) 都是一个 DFA
• Magical: 想象成 machine 在每一个 nondeterministic step 猜测要往哪个方向走，并且总是能猜测正确

从上面的 mathematical way 结合前面提到的 union operation 的封闭性的证明，不难看出将所有分支对应的 DFA 进行 "union" 操作得到的新的 DFA 其实就是这个 NFA，也就是说，每个 NFA 都可以被转化为一个等价的 DFA。

Theorem

Every nondeterministic finite automaton has an equivalent deterministic finite automaton.

进而我们可以得到以下定理：

Theorem

If an NFA recognizes \(A\) then \(A\) is regular.

Proof

令 NFA \(M=(Q, \Sigma, \delta, q_0, F)\) recognizes \(A\)，我们需要构造能 recognize \(A\) 的 DFA \(M^{\prime}=(Q^{\prime}, \Sigma, \delta^{\prime}, q_0^{\prime}, F^{\prime})\)

Idea: DFA \(M^{\prime}\) keeps track of the subset of possible states in NFA \(M\).

Construction:

• \(Q^{\prime}=\mathcal{P}(Q)\)
• \(\delta^{\prime}(R, a)=\)
• \(q_0^{\prime}=\{q_0\}\)
• \(F^{\prime}=\{R|R\text{ intersects }F\}\)

再结合以上两个定理，我们又可以得到

Corollary

A language is regular if and only if some nondeterministic finite automaton recognizes it.

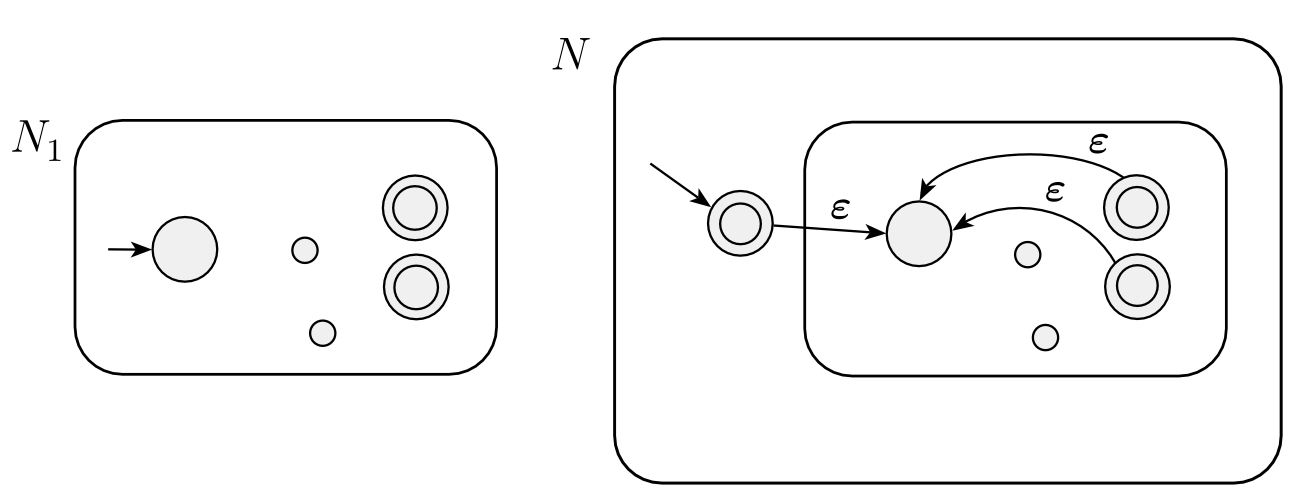
回到前面关于 regular operations 的封闭性的证明，有了 NFA，证明它们会更简单且直观。

Proof

union:

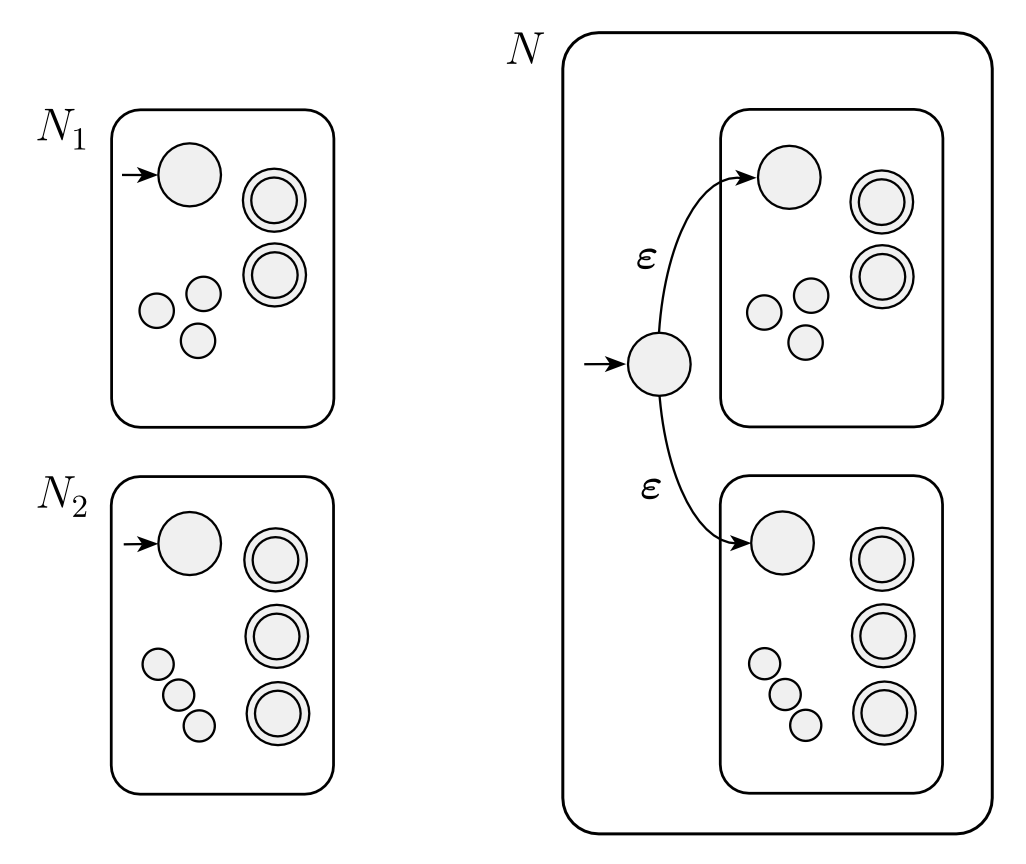
concatenation:

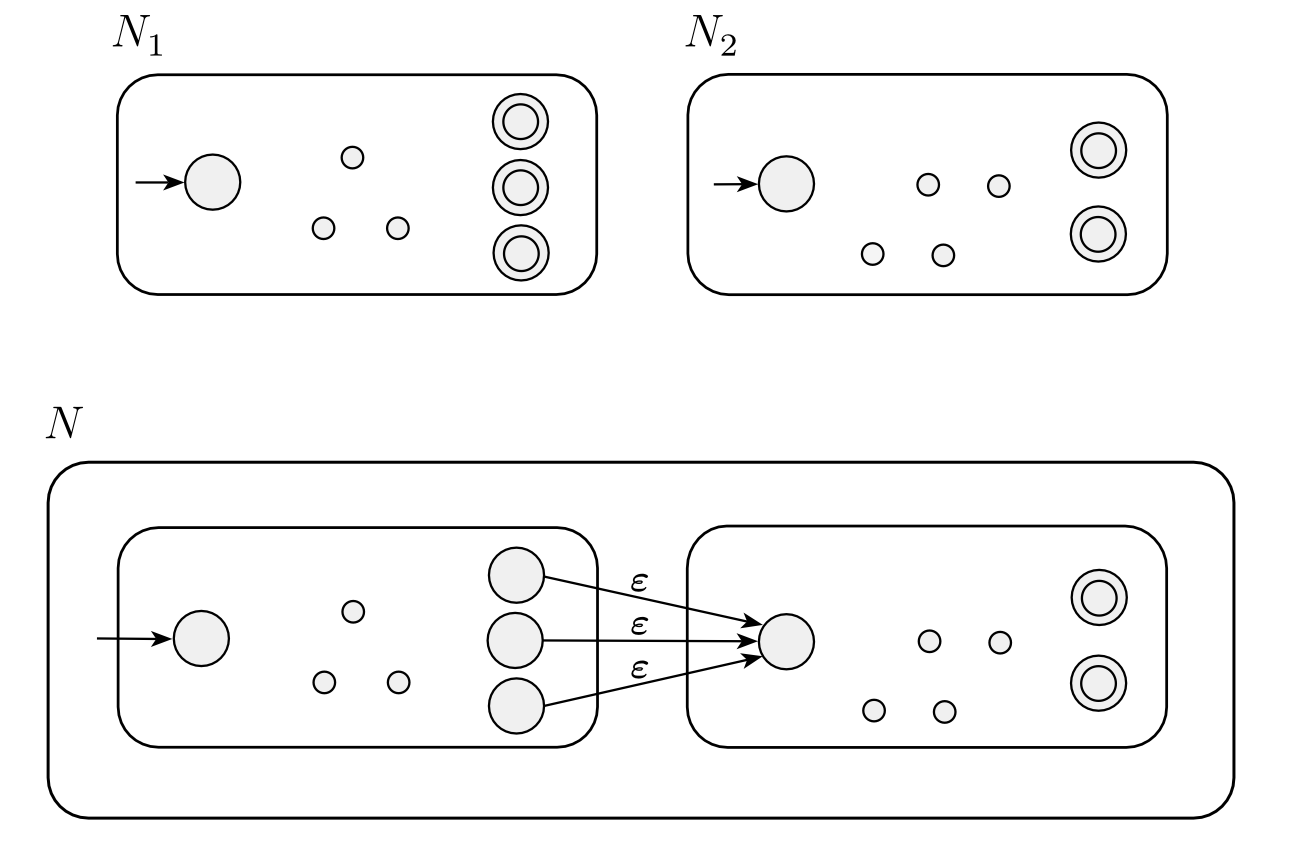
star:

Regular Expressions

类似于数学中用算数表达式来表示一个数字，我们也可以利用 regular operations 构造 languages 的表达式，称为 regular expressions.

Definition

Say that R is a regular expression if R is

1. \(a\) for some \(a\) in the alphabet \(\Sigma\),
2. \(\epsilon\),
3. \(\varnothing\),
4. \(R_1\cup R_2\), where \(R_1\) and \(R_2\) are regular expressions,
5. \(R_1\circ R_2\), where \(R_1\) and \(R_2\) are regular expressions, or
6. \((R_1^{\ast})\), where \(R_1\) is a regular expression.

regular expression 是 programming languages 中很重要的一个模型，当一个 PL 的 syntax 可以用 tokens 组成的 regular expressions 来表示，automatic system 就可以生成 lexical analyzer 来处理一个 input program.

由于 regular operations 可以表示 languages，而 regular language 又可以被 NFA 定义，于是我们有

Theorem

If \(R\) is a regular expression and \(A=L(R)\) then \(A\) is regular.

Proof

将 \(R\) 转化为一个等价的 NFA \(M\).

Idea: regular expression 的定义是 inductive definition，于是我们同样可以利用它的定义进行 inductive proof，将复杂的证明转化为简单的几个小证明。

分为两种情况证明：

1. If \(R\) is atomic:
   

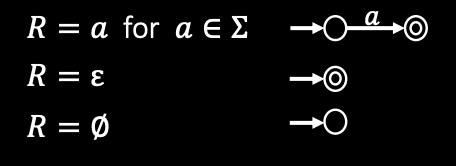
2. If \(R\) is composite:
   

反过来也是一样的：

Theorem

If \(A\) is regular then \(A = L(R)\) for some regular expr \(R\).

要证明这个定理，我们先引入 Generalized NFA (GNFA) 的概念，它应用了前一个的定理，将 regular expr 融入进 NFA 中，简化了 NFA 的形式，这也可以启发我们不断减少 NFA (GNFA) 的 states 是可以将 NFA (GNFA) 转化为 regular expr 从而也就证明了这个定理。

Definition

A Generalized Nondeterministic Finite Automaton (GNFA) is similar to an NFA, but allows regular expressions as transition labels.

Proof

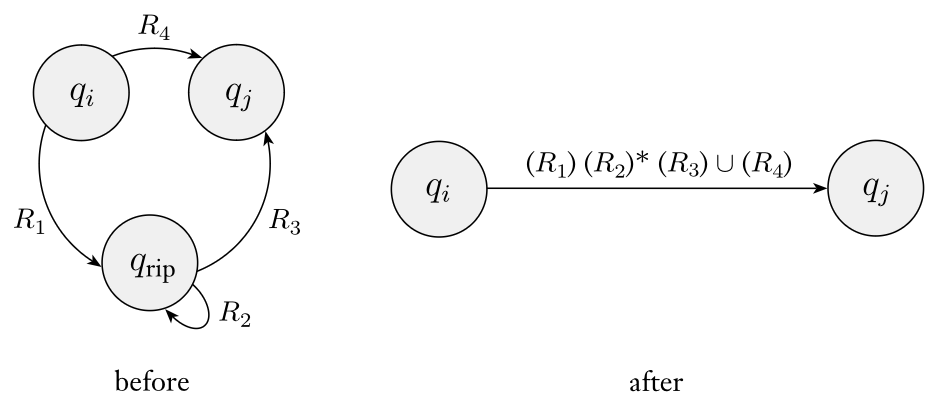
考虑 induction.

• Basis (\(k=2\)):
  • 
• Induction step (\(k>2\)):
  • 由 \(k-1\) 增加 state 到 \(k\) 并不方便，不妨反过来证明 \(k\) 个 states 的 GNFA 去掉一个 state 得到的 GNFA 是等价的
  • 

Abstract

What can regular languages express?

• Languages that requiring counting modulo a fixed integer.
• Intuition: A finite automaton that runs long enough must repeat states.（这一点从后面的 pumping lemma 也可以看出来）
• Finite automaton cannot remember # of times it has visited a particular state.

Nonregular Languages

根据直觉来判断某个 language 是否是 regular 的是不靠谱的。pumping lemma 是一个 regular language 具有的必要条件，是判断 nonregular languages 的好工具。

Lemma

If \(A\) is a regular language, then there is a number \(p\) (the pumping length) where if \(s\) is any string in \(A\) of length at least \(p\), then \(s\) may be divided into three pieces, \(s = xyz\), satisfying the following conditions:

1. for each \(i\ge 0\), \(xy^i z\in A\),
2. \(|y|>0\), and
3. \(|xy|\le p\).

注意到 finite automata 中的 "finite"，考虑 NFA 的 diagram 的形式，从 start state 到任何一个 accept state 的最长路径（存在环的话就计算一次环的长度）长度必然是有限的，取最长的长度，记为 \(p\)，那么 \(p\) 就是这个 NFA 的 pumping length。如果一个长度大于 \(p\) 的 string 可以被 accept，这说明它对应的路径中必然存在环，而且这个环被计算过多次，也就是 pumping lemma 中的 \(y\)。

Context-Free Languages

regular languages 的力量终究还是有限的，某些规则简单的语言仍然不能被 finite automata 或 regular expr 来描述，而 context-free grammars 则引入了递归的概念，这使得它的表示能力更为强大。

Context-Free Grammars

CFG 由 substitution rules (productions) 组成，根据这些 rules 进行一系列 substitutions 得到一个 string 的过程被称为 derivation，例如

\[ A\Rightarrow 0A1\Rightarrow 00A11\Rightarrow 000A111\Rightarrow 000B111\Rightarrow 000\#111 \]

derivation 也可以被表示为树形结构，称为 parse tree 。

所有能被 CFG 生成的 string 的集合被称为 language of the grammar，能被 CFG 生成的 languages 称为 context-free language (CFL)

Definition

A context-free grammar is a 4-tuple \((V, \Sigma, R, S)\), where

1. \(V\) is a finite set called the variables,
2. \(\Sigma\) is a finite set, disjoint from \(V\), called the terminals,
3. \(R\) is a finite set of rules (rule form: \(V\to (V\cup \Sigma)^\ast\)),
4. \(S\in V\) is the start variable.

对于 \(u, v\in (V\cup \Sigma)^\ast\) ，如果 \(u\) 通过一步替换即可得到 \(v\)，就写作 \(u\Rightarrow v\)，读作 \(u\) yields \(v\)，如果多步替换得到，就写作 \(u\xRightarrow{\ast}v\)，读作 \(u\) derives \(v\)，进而 the languages of the grammar 可以表示为 \(\{ w\in\Sigma^\ast\mid S\xRightarrow{\ast}w \}\).

给定一个 language，比起之前构造出对应的 finite automaton，构造它的 CFG 会相对更困难、更需要创造力，因为我们已经习惯了针对某些特定的任务设计一个 machine，而 CFG 则更近似于描述这个 language（和 procedural languages like C++ v.s. declarative languages like SQL 有点像🤔），想要设计一个 CFG 可以遵循以下几点建议：

• 将 CFL 拆分成一些简单的 CFLs，分别对这些 CFLs 设计 CFG 最后将这些 CFGs 结合
• 如果这个 language 是 regular language，就先设计一个 DFA，再按照以下步骤将 DFA 转换为 CFG
  • Make a variable \(R_i\) for each state \(q_i\) of the DFA.
  • Add the rule \(R_i \to aR_j\) to the CFG if \(\delta(q_i,a) = q_j\) is a transition in the DFA.
  • Add the rule \(R_i \to \epsilon\) if \(q_i\) is an accept state of the DFA.
  • Make \(R_0\) the start variable of the grammar, where \(q_0\) is the start state of the machine.
• 像 \(\{ 0^n 1^n\mid n\ge 0 \}\) 这样两个 substrings 的信息要对应并且可能无限长的 language，熟练使用 \(R\to uRv\) 这种 rule

在某些时候，设计出来的 CFG 可能对同一个 string 有不同的 derivation，这种 property 称为 ambiguity.

Definition

A string \(w\) is derived ambiguously in context-free grammar \(G\) if it has two or more different leftmost derivations. Grammar \(G\) is ambiguous if it generates some string ambiguously.

值得注意的是，某些 languages 只能由 ambiguous CFG 生成，这种 languages 被称为 inherently ambiguous (e.g. \(\{a^i b^j c^k\mid i=j\text{ or }i=k \}\)).

Chomsky normal form 是一种简单、统一的 CFG rule form.

Definition

A context-free grammar is in Chomsky normal form if every rule is of the form

\[ \begin{align} A &\to BC \nonumber \\ A &\to a \nonumber \end{align} \]

where \(a\) is any terminal and \(A\), \(B\), and \(C\) are any variables—except that \(B\) and \(C\) may not be the start variable. In addition, we permit the rule \(S \to \epsilon\), where \(S\) is the start variable.

Pushdown Automata

去掉各个状态结点的细节，NFA 可以简单地抽象为下图的形式：

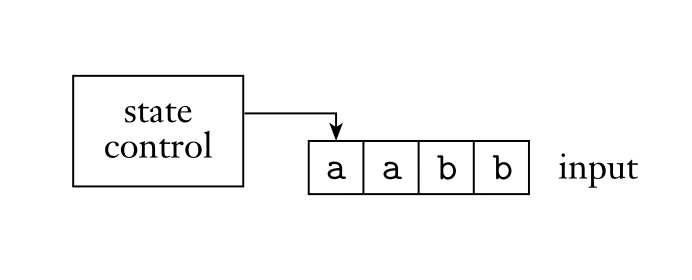
而 pushdown automaton 与 NFA 相似，但是加上了一个 stack 使得它具备了记忆的功能。

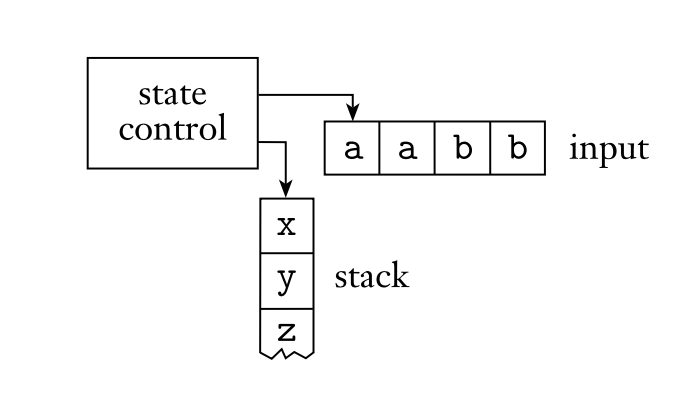
Definition

A pushdown automaton is a 6-tuple \((Q, \Sigma, \Gamma, \delta, q_0, F )\), where \(Q\), \(\Sigma\), \(\Gamma\), and \(F\) are all finite sets, and

1. \(Q\) is the set of states,
2. \(\Sigma\) is the input alphabet,
3. \(\Gamma\) is the stack alphabet,
4. \(\delta\colon Q \times \Sigma_{\epsilon} \times \Gamma_{\epsilon}\to P(Q \times \Gamma_{\epsilon})\) is the transition function,
5. \(q_0 \in Q\) is the start state, and
6. \(F \subseteq Q\) is the set of accept states.

前面学到过 finite automaton 和 regular expression 是等价的，因此不难想到： pushdown automaton 是否和 CFG 也是等价的？

尽管 pushdown automaton 的特点在于 stack 的存在使其具有了 memory，而 CFG 则是借助了 recursion 的力量，看似不相关联，但是回想一下 CS61A 中介绍 recursion 时，递归函数内部实现其实就是将 function frames 以 stack 的形式存储下来，这样看来，二者之间的等价关系也并不是什么奇怪的事了。

Theorem

A language is context free if and only if some pushdown automaton recognizes it.

先证必要性：

Lemma

If a language is context free, then some pushdown automaton recognizes it.

Proof

Proof idea: 显然是将 CFG 转换为 pushdown automaton.

观察 parse tree，可以发现自下而上看的话，这个过程就好比于在 stack 中不断 match、pop 的过程，那么转换过程就很好想了。

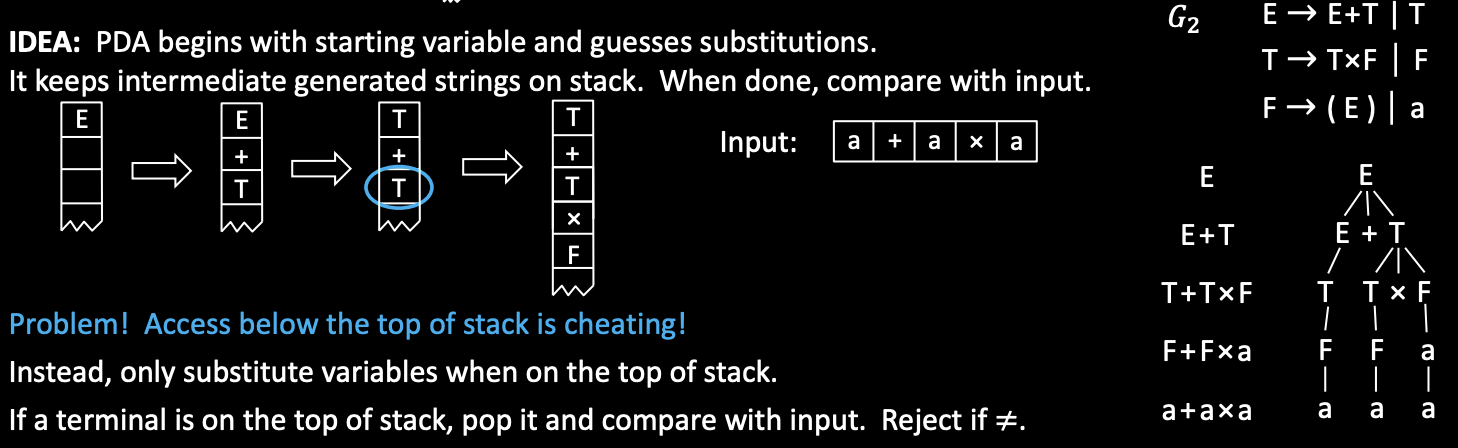
Proof construction: convert the CFG for \(A\) to the following PDA.

1. Push the start symbol (\(E\)) on the stack.
2. If the top of stack is:
   • Variable: replace with the right hand side of rule (nondet choice).
   • Terminal: pop it and match with next input symbol.
3. If the stack is empty, accept.

然后证充分性：

Theorem

If a pushdown automaton recognizes some language, then it is context free.

Proof

反过来其实就是上一个证明的逆过程。

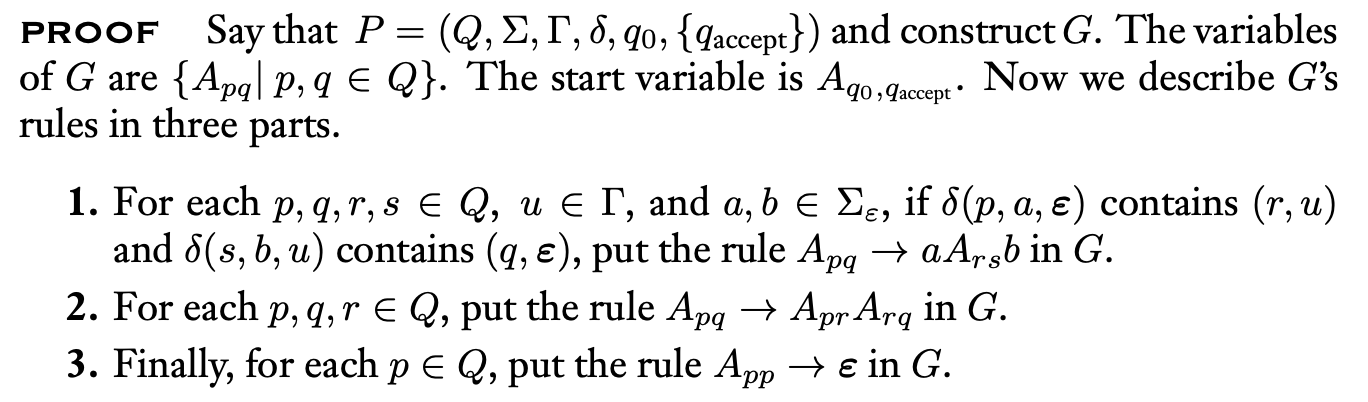
最后，由前面提到的 DFA 转化为 CFG 的步骤，不难看出 regular languages 和 context-free languages 的关系：

Corollary

Every regular language is context free.

Non-Context-Free Languages

和 finite automata 一样，CFG 尽管借助递归的力量拥有了更强大的表达能力，但是仍然有所限制，它所能识别的字符串中除了有限长的字符串都必然会有至少两个子串是“重复”的，这样是符合递归的定义的，于是 CFL 也会一个 pumping lemma.

Pumping lemma for context-free languages

If \(A\) is a context-free language, then there is a number \(p\) (the pumping length) where, if \(s\) is any string in \(A\) of length at least \(p\), then \(s\) may be divided into five pieces \(s = uvxyz\) satisfying the conditions

1. for each \(i\ge 0\), \(uv^ixy^iz\in A\),
2. \(|vy|>0\), and
3. \(|vxy|\le p\).

从 parse tree 上很容易看出它的正确性：

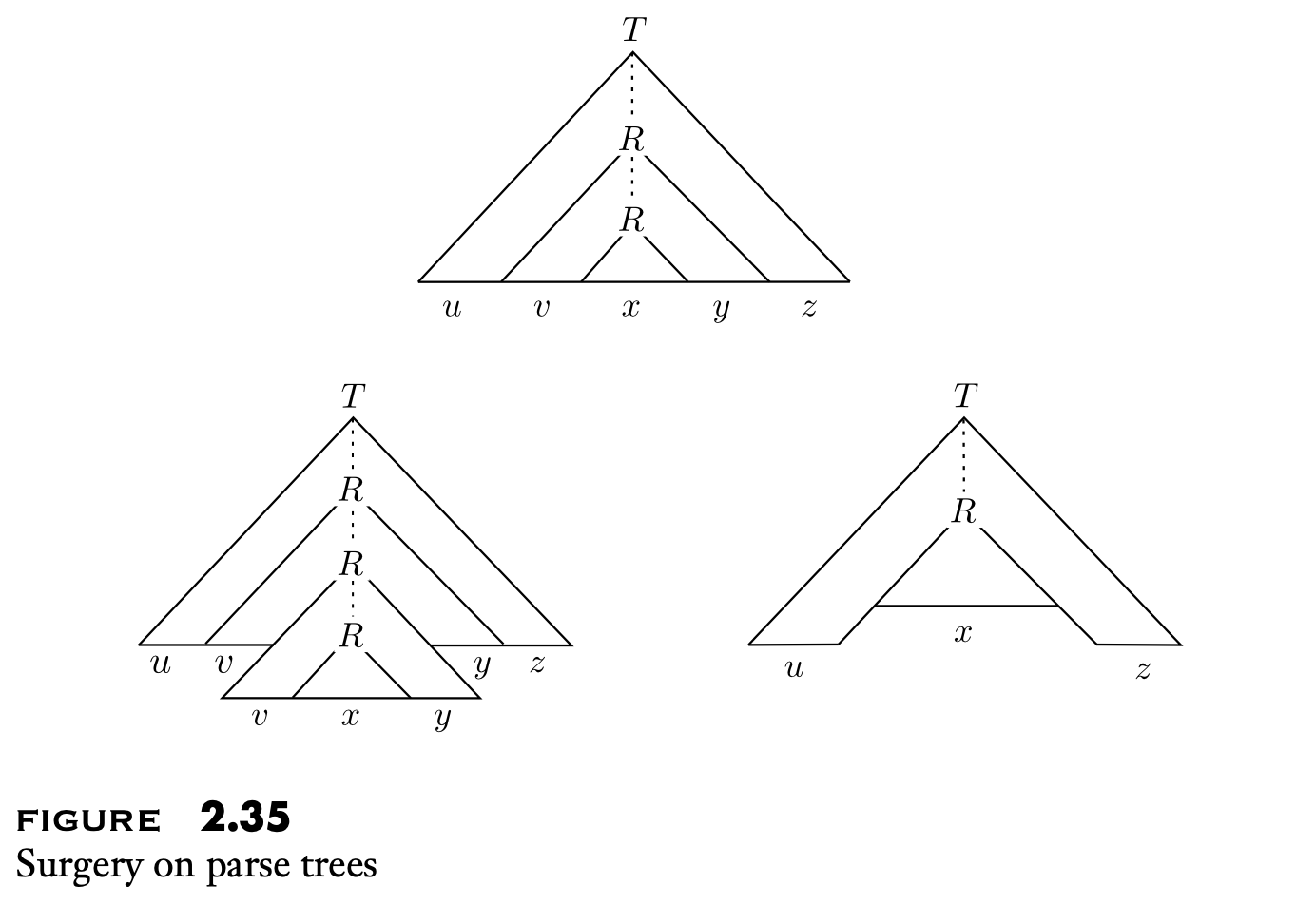
Deterministic Context-Free Languages

在前面的 regular languages 中，我们知道 DFA 和 NFA 的表达能力是一样的，nondeterminism 的力量在 regular languages 中并没有得到体现（不过 NFA 一般会比 DFA 好构造得多 qwq ），但是在 CFL 中，nondeterminism 给 PDA 带来了新的活力。

Thoughts on the essence

为什么 nondeterminism 在 CFL 中可以有用武之地而在 regular languages 中却像是花瓶一样的存在呢？它们的本质区别究竟在于何处？

我们可以在某种程度上，狭义地认为这是 finiteness 造成的。

在 finite automata 中，无论是 states 还是 transitions 都是 finite 的，因而 DFA 可以通过 subset construction algorithm 转化为 NFA，nondeterminism 在其中等价于 more options，允许了 NFA 对于一个 input symbol 可以有多个 transitions，但是 possible states 和 transitions 终究还是 finite，可以被 DFA 通过增加 states 追赶上来，因此 nondeterminism 提供的力量相当有限。

而在 CFG 中，一个 symbol 对应多个 rule，每个 rule 都可以被重复使用，使得它的 states 是 infinite 的，同时也会产生一定的 complexity 使其区别于 regular languages。在这种情况下，nondeterminism 的引入带来的是 more parsing paths，使得同一个 string 可以被不同的结构所表示，这也引入了 ambiguity，这些 ambiguous CFLs 是无法被 DPDA 所识别的。

值得注意的是，nondeterminism 只是 opens the door for ambiguity，这并不代表所有 NCFL 都是 ambiguous 的。

• DCFLs \(\subset\) unambiguous CFLs
• ambiguous CFLs \(\subset\) NCFLs

这一个 section 可以算是一个 bonus section，对于 CFL 的理论更深入、复杂，我只是看了其中很小一部分内容，并且思考了 nondeterminism 在 regular languages 和 CFLs 中各自发挥的本质作用，剩余的内容是否会在之后的某一天接着学习仍然是 nondeterministic 的（逃

非常好 nondeterminism，使我的 TCS 旋转

red pink purple deep purple indigo blue light blue cyan teal green light green lime yellow amber orange deep orange brown grey blue grey black white

Comments