The Church-Turing Thesis
finite automata 对于只有很少的 memory 的 devices 来说是一个很好的 model,而 pushdown automata 则对具有 unlimited memory 并且只以 FIFO 的方式使用的 devices 来说也是一个很好的 model,但是对于有 general purpose 的 computers 来说就显得过于无力了。
Turing Machines¶
Turing machine 在 finite automata 的基础上加入了 unlimited & unrestricted memory,这使它的表达能力更加强大,不过也会有些无法处理的问题(例如 halting problem)
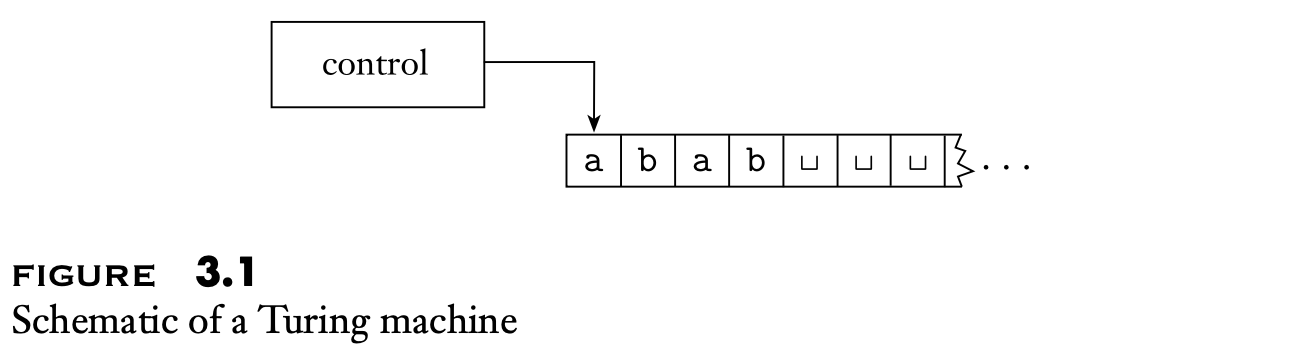
Turing machine 相比于 finite automata,有以下几点不同:
- Turing machine 对 tape 可读可写
- read-write head 可在 tape 上任意方向移动
- tape 是 infinite 的
- accept & reject states 会立即生效
Turing machine 的 formal definition 如下,
Definition
A Turing machine is a 7-tuple, \((Q, \Sigma, \Gamma, \delta, q_0, q_{accept}, q_{reject})\), where \(Q, \Sigma, \Gamma\) are all finite sets and
- \(Q\) is the set of states,
- \(\Sigma\) is the input alphabet not containing the blank symbol ␣,
- \(\Gamma\) is the tape alphabet, where ␣ \(\in \Gamma\) and \(\Sigma \subseteq \Gamma\),
- \(\delta\colon Q\times \Gamma \to Q\times \Gamma \times\{L,R\}\) is the transition function,
- \(q_0 \in Q\) is the start state,
- \(q_{accept} \in Q\) is the accept state, and
- \(q_{reject} \in Q\) is the reject state, where \(q_{reject} \not= q_{accept}\).
在 Turing machine 计算的过程中,目前的状态 (\(q\))、tape 的内容 (\(uv\)) 以及 head 的位置 (points to \(v\)) 会发生改变,我们将这三者称为 a configuration of the Turing machine,写作 \(u\, q\, v\),相当于 Turing machine 整体所处的 state.
所有能被 Turing machine \(M\) 识别的 strings 的集合称为 the language of \(M\),写作 \(L(M)\).
Definition
Call a language Turing-recognizable if some Turing machine recognizes it.1
给定一个 input,Turing machine 可能会产生三种结果:accept, reject or loop. 永远不会 loop 的 machine 被称为 deciders ,因为它们永远会决定一个 input 究竟是 reject 还是 accept. 当一个 decider 能够 recognize some language 时,我们称其为 decide that language.
Definition
Call a language Turing-decidable or simply decidable if some Turing machine decides it.2
TM Variants¶
Info
意识到自动机理论部分的进度拖的太慢,而且这部分过于传统以至于让人感到十分无聊,因此不再赘述
The Definition of Algorithm¶
The Church-Turing thesis