Data Flow Analysis

Info

南京大学「软件分析」课程 Data Flow Analysis 部分的学习笔记。

Data Flow Analysis - Applications¶

Overview of Data Flow Analysis¶

data flow analysis 的核心就是 how data flows on CFG?，将这句话拆开了讲就是：

how application-specific data：对数据的 abstraction，例如 +、-、0 等
flows through the：根据分析的类型作出 approximation
may-analysis: outputs information that may be true. 是一种 over-approximation，也是大多数静态分析采用的类型
must-analysis: output information that must be true. 是一种 under-approximation
nodes and: 数据如何 transfer，用 transfer function 表示，例如 + op - = - 等
edges of: 数据流如何处理，例如两个控制流汇入一个结点
CFG

Preliminaries of Data Flow Analysis¶

Each execution of an IR statement transforms an input state to a new output state.

Every input/output state is associated with a program point, corresponds to an edge of CFG.

对于每一个 program point，我们用一个 data-flow value 表示对于当前所有可能的 program states 的 abstraction。

transfer function's contraints: 分为 forward analysis 和 backward analysis 两种，用 \(f_s\) 表示经过 definition \(s\) 的 transfer function
control flow's contraints:
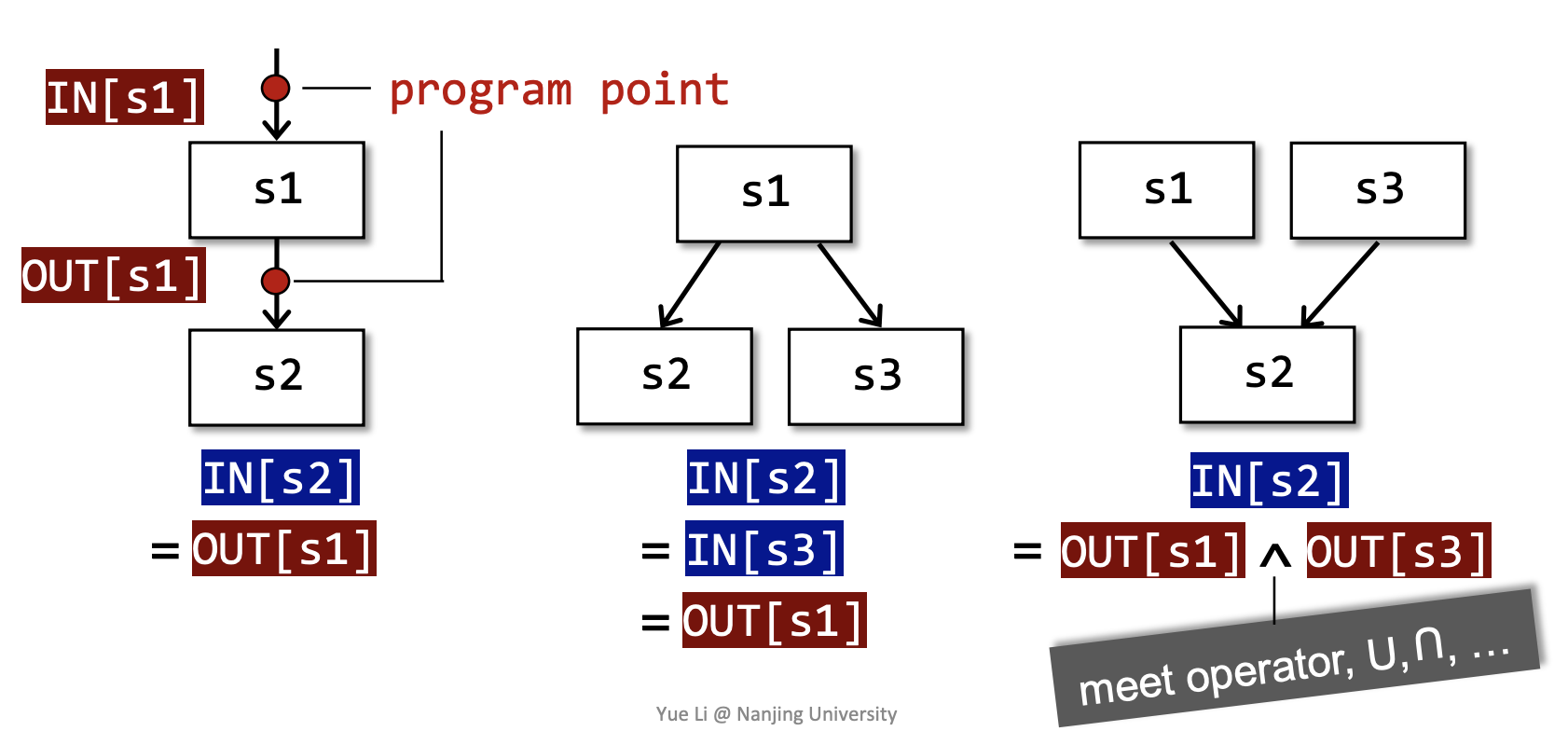
within a BB: IN[\(s_{i+1}\)] = OUT[\(s_i\)]
among BBs: OUT[B] = \(f_B(\)IN[B]\()\)，其中 \(f_B\) 是 \(f_{s_i}\) 的复合函数

Reaching Definitions Analysis¶

为了减少复杂性，这里的 RDA 不包括 method calls 和 aliases。

一个 definition \(d\) 可以 reach program point \(q\) 当且仅当存在一条路径 \(p\) 到 \(q\) 使得 \(d\) 不会在这条路径上被 kill 掉。

对于变量 \(v\) 的 definition 就是指对 \(v\) 的赋值语句，如果原来的 definition \(d_1\) 对 \(v\)，经过的某个 BB 中有另一个 \(d_2\) 也对 \(v\) 进行了赋值，那么就说 \(d_1\) 被 kill 掉了。

在 reaching definition analysis 中，data flow value 被设置为长度与 definitions 的数量相等的 bit vector，每个 bit 对应一个 definition，0/1 表示到达这个 program point 时对应的 definition 是否被 kill 了。

由于每个 definition 都被定义为独一无二的，所以每经过一个 BB 就会“产生新的 definition”，因此 transfer function 被定义为 \(\mathrm{OUT[B]}=gen_B\cup(\mathrm{IN[B]}-kill_B)\)。

RDA 的 algorithm 如下图所示：

由于 \(gen_B\) 和 \(kill_B\) 是始终不变的，因此只要 \(\mathrm{IN[B]}\) 不变那么 \(\mathrm{OUT[B]}\) 也一定不会变。每次经过一轮迭代，上一轮 \(\mathrm{IN[B]}\) 中为 1 的 bit 仍然会是 1，从而 \(\mathrm{IN[B]}\) "never shrinks"，因此 \(\mathrm{OUT[B]}\) 也会是 "never shrinks" 的，而 bit 的数目是有限的，所以 \(\mathrm{OUT[B]}\) 迟早会 reach a fixed point，从而这个算法一定可以终止。

Live Variables Analysis¶

如果存在一条以 program point \(p\) 为起点的路径，使得 variable \(v\) 在这条路径上能够被使用（\(use(v)\)），同时没有在被使用前 redefined，就称 \(v\) is live at \(p\)，否则就称 \(v\) is dead at \(p\).

LVA 对于 data flow values 的设置是与 RDA 类似的，只是将 definition 换成了 variable。

基于以上定义，LVA 的 algorithm 是一种 backward analysis，我们根据 \(\mathrm{OUT[B]}\) 来求出 \(\mathrm{IN[B]}\)，对应的 transfer function 为 \(\mathrm{IN[B]}=use_B\cup(\mathrm{OUT[B]}-def_B)\)。

LVA 的 algorithm 如下图所示：

Available Expressions Analysis¶

表达式 x op y(\(e\)) 在 program point \(p\) 是 available 的当且仅当以下两个条件成立：

从 Entry 到 \(p\) 的所有路径都需要经过 the evaluation of \(e\)
在经过最后一次 evaluation of \(e\) 之后没有再对 \(x\) 或者 \(y\) 进行 redefine

AEA 的 flow data values 也是 bit vector 的形式。

显然 AEA 中的 \(gen_B\) 是指 B 中新的 expression，\(kill_B\) 指的是 B 中对 \(\mathrm{IN[B]}\) 的 expressions 的 variables 的 redefine 语句。

AEA 允许我们在有多条路径可以到达 \(p\) 时，无需重复计算 expression \(e\)，而是直接用 last evaluation of \(e\) 的值进而达到优化的目的。

从 AEA 的定义中，不难看出这是一种 must-analysis，并且 \(\mathrm{IN[B]}\) 需要取的是前继的交集。

AEA 的 algorithm 如下图所示：

需要注意的是，\(\mathrm{OUT[B]}\) 的初始化与前面的 may-analysis 是不同的。

	Reaching Definitions	Live Variables	Available Expressions
Domain	Set of definitions	Set of variables	Set of expressions
Direction	Forwards	Backwards	Forwards
May/Must	May	May	Must
Boundary	OUT[entry]=∅	IN[exit]=∅	OUT[entry]=∅
Initialization	OUT[B]=∅	IN[B]=∅	OUT[B]=U
Transfer function	\(\mathrm{OUT[B]}=gen_B\cup(\mathrm{IN[B]}-kill_B)\)	\(\mathrm{IN[B]}=use_B\cup(\mathrm{OUT[B]}-def_B)\)	\(\mathrm{OUT[B]}=gen_B\cup(\mathrm{IN[B]}-kill_B)\)
Meet	\(\cup\)	\(\cup\)	\(\cap\)

Data Flow Analysis - Foundations¶

Iterative Algorithm, Another View¶

在前面 DFA 的迭代算法中，以 forward analysis 为例，假设一共有 k 个 node，每次迭代后所有的 \(\mathrm{OUT[B]}\) 可以抽象为一个 k-tuple，令 domain 为 \(V\)，迭代的过程可以看作一个函数 \(F\colon V^k\to V^k\)，而迭代的出口就是到达这个函数的不动点 \(X=F(X)\)。

由以上的抽象，我们可以考虑几个问题：

这个函数是否一定存在不动点？
是否会存在多个不动点？如果是，我们的算法求出的不动点是否是最优解？
什么时候才能到达不动点？

Data Flow Analysis Framework via Lattice¶

一个 data flow analysis framework \((D,L,F)\) 由以下几个部分组成：

\(D\): forward / backward analysis
\(L\): lattice, includes the domain and the meet/join operator
\(F\): a family of transfer functions from \(V\) to \(V\)

从 lattice 的角度来看，data flow analysis 的算法相当于迭代地在一个 lattice 上运用 transfer function 和 meet/join 操作。

Monotonicity and Fixed Point Theorem¶

再回到前面提出的几个问题。

由 \(\mathrm{OUT}\) 是 "never shrinks" 的性质，我们可以推出这个 transfer function 一定存在不动点。

关于第二个问题，仅仅从函数的角度上考虑，一个函数的不动点实则是它与直线 \(y=x\) 的交点，那么很显然，不动点是可能存在多个的。

但是这里的函数是 lattice 上的函数，自然也会具有一些特性。

monotonicity: 如果函数 \(f\colon L\to L(L\ is\ a\ lattice)\) 满足任给 \(x,y\in L\)，有 \(x\le y\rArr f(x)\le f(y)\) 就称它是 monotonic 的
fixed point theorem: 对于一个 complete lattice \((L,\le)\)，如果 \(L\) 上的函数 \(f\) 是 monotonic 的，并且 \(L\) 是 finite 的，那么
最小的 fixed point 可以通过不断迭代 \(f(\bot),f(f(\bot)),\dots,f^k(\bot)\) 直到 reach a fixed point 的方式找到
最大的 fixed point 可以通过不断迭代 \(f(\top),f(f(\top)),\dots,f^k(\top)\) 直到 reach a fixed point 的方式找到

证明 fixed point theorem 可以分为以下两个部分进行证明：

existence of fixed point: 由于 \(f\) 是 monotonic 的，因此我们对 \(\bot\) 进行每次迭代的值都是递增的，而这个 lattice 又是 finite 的，那么一定会达到一个最大值不动，这个最大值就是一个不动点，对 \(\top\) 做的迭代也是类似的。
least fixed point: 反证法。假设 \(x\) 是最小的 fixed point，由 \(\bot\) 的定义，必然有 \(\bot \le x\)，然后对两边一直做迭代，左边会达到一个非最小的不动点 \(p\)，右边仍然是 \(x\)，由 monotonicity 的定义可知，\(p\le x\)，这与 \(x\) 是最小的 fixed point 的假设矛盾，因此 least fixed point 的算法是正确的，同理，greatest fixed point 的算法也是正确的。

我们之前设计的 DFA 的算法都是从 \(\bot\) 或者 \(\top\) 开始迭代，因此求出的不动点一定是 least/greatest fixed point，在某些定义上可以认为我们的算法求出来的是最优解。

以上关于函数性质的论证都是基于 lattice 的，要证明我们的 DFA 迭代算法也有同样的性质，还需要（尽可能）将我们的算法与 fixed point theorem 建立关联。

Relate Iterative Algorithm to Fixed Point Theorem¶

根据 fixed point theorem 的条件，我们首先 relate iterative algorithm 中的 fact 和 lattice。

假设有 \(k\) 个 node，那么经过 \(i\) 轮迭代后得到的 fact 的形式为 \((v_1^i,v_2^i,\dots,v_k^i)\)，对于 node \(j\)，每轮迭代产生的 \(v_j^i\) 组成的集合与集合的 \(\subset\) 关系可以看作一个 finite 且 complete 的 lattice \(L\)，从而整个 fact 就是这些 lattice 的笛卡尔积 \(L^k\)，从而 fact 也是一个 finite 且 complete 的 lattice。

之后只需 relate transfer + meet/join function 与 monotonic 的函数 \(f\colon L\to L(L\ is\ a\ lattice)\)。

从前面证明 \(\mathrm{OUT}\) 是 never shrinks 的过程中，我们已经可以知道 transfer function 是满足 monotonic 的条件的了。而对于 meet/join function，我们根据 monotonic 的定义可以很简单的证明。

因此，我们可以 relate the algorithm to the fixed point theorem。也就可以很自信的认为对前两个问题的回答是正确的了。

现在我们回答第三个问题。我们定义 lattice 的高度是从 \(\top\) 到 \(\bot\) 的最长路径的长度，假设单个结点的 lattice 的高度是 \(h\)，CFG 的结点数为 \(j\)，每次迭代至少可以让一个结点往上爬一个高度，所以最坏的情况下的迭代次数是 \(h\cdot k\)。

May and Must Analysis, a Lattice View¶

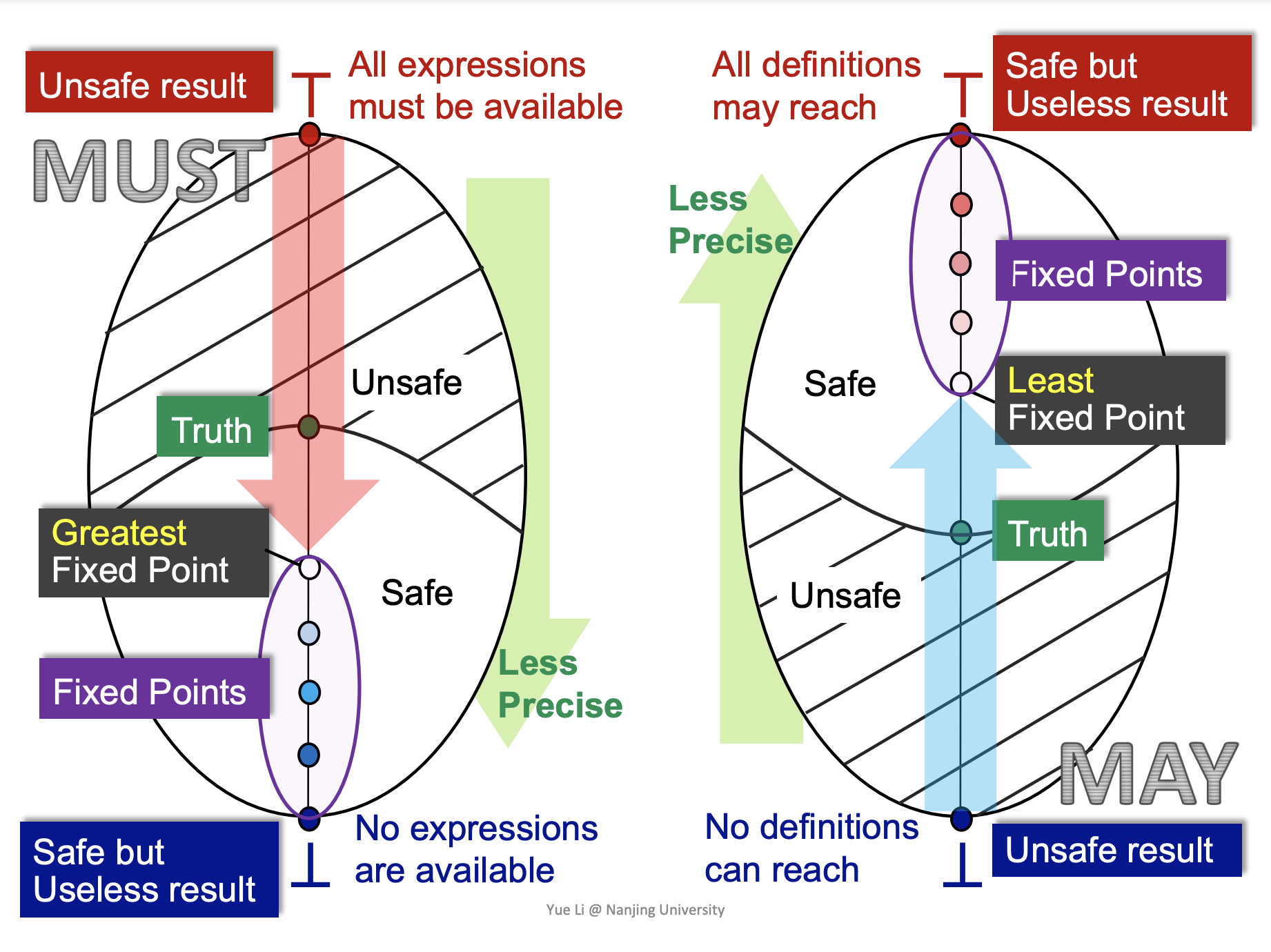
MOP and Distributivity¶

Meet Over All Paths Solution (MOP) 是考虑所有可能到达结点 \(s_i\) 的路径，将这些路径的 OUT 取 meet/join 来得到 \(s_i\) 的 IN 或者说 MOP[\(s_i\)]，也就是根据所有路径的计算结果取 lub/glb。

但是 CFG 中某些 path 是 not executable 的，也会有 unbounded、not enumerable 的路径，所以显然 MOP 是 not fully precise、impractical 的。

对比 iterative algorithm，可以发现我们算法的形式是 \(F(x\cup y)\) 的，而 MOP 的形式是 \(F(x)\cup F(y)\) 的，由 \(F\) 是 monotonic 的和 lattice 的性质可以推出 \(F(x)\cup F(y)\le F(x\cup y)\) ，所以 iterative algorithm 的精度是不如 MOP 的。

但是，当 \(F\) 是 distributive 时，iterative algorithm 的精度是和 MOP 一样的。再分析 iterative algorithm 的 \(F\)，可以发现 bit-vector 或 gen/kill problems 都是 distributive 的，所以前面介绍的几种算法精度都是与 MOP 相当的。

Constant Propagation¶

决策在 program point \(p\) 的一个 variable \(x\) 是否是一个常量的问题就是 constant propagation。

direction: forward analysis
lattice:
OUT: a set of pairs \((x,v)\)
domain of \(v\): UNDEF / values(-2, -1, 0...) / NAC
\(\cap\):
- NAC \(\cap\) \(v\) = NAC
- UNDEF \(\cap\) \(v\) = \(v\)
transfer function: \(F\colon \mathrm{OUT}[s]=gen\cup (\mathrm{IN}[s]-\{(x,\_)\})\)
s: x = c or x = y or x = y op z

从下图中的简单例子可以看出 constant propagation 的 \(F\) 是 non-distributive 的：

Worklist Algorithm¶

worklist algorithm 实现了对 iterative algorithm 的优化：如果经过一个 BB，它的 IN 没有变化，那么之后这个 BB 的 OUT 一定不会变化。因此，我们只需维护一个 worklist of BBs，如果当前的 BB 的 OUT 发生了变化，我们才将它所有的后继加入 worklist。